压缩编码

当我们以数字形式表示信息，比如一幅图像，意味着我们必须将其切分成微小的片段。这样我们就可以将图像发送为一系列颜色符号，而这些颜色可以用一些代码表示为唯一的数字。

考虑以下挑战。爱丽丝和鲍勃可以用二进制传输和接收消息（摩尔斯电码）。他们向客户收费每位一便士来使用他们的系统，一位常规客户要发送一条消息，消息长度为1,000个符号。消息的含义完全未知。通常，这会使用标准的2位编码发送，导致收费2,000位。

然而，爱丽丝和鲍勃之前已经对这位客户进行了一些分析，并确定了消息中每个符号的概率不同。他们能否利用这些已知的概率来压缩传输并增加他们的利润？什么是最优的编码策略？

大卫·赫夫曼在1952年提供了著名的最优策略，并基于自底向上构建二叉树。首先，我们可以列出所有在底部的符号，我们可以称之为节点。然后我们找到两个最不可能的节点，本例（A是$50%$，B是$12.5%$，C是$12.5%$，D是$25%$）中为B和C，并将它们合并成一个，并将概率相加。然后我们重复这个过程，直到最不可能的节点只剩下一个。最后，在这棵树上标记边缘为任意顺序的0或1。

这个动态过程很难用图像表示，最好是靠视频理解


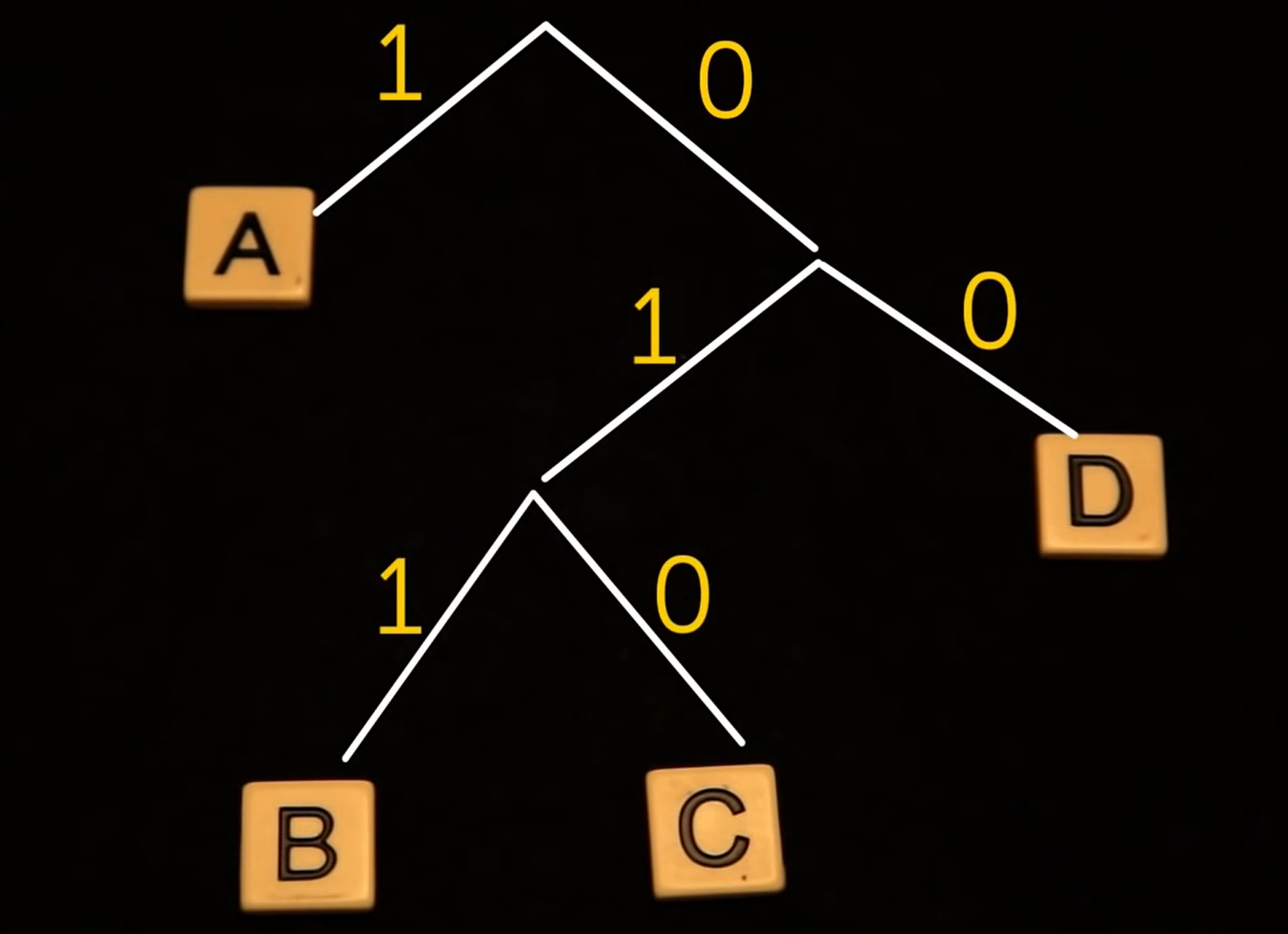
现在，每个字母的编码只是从树顶到给定字母的路径。因此，对于A，它只是一条边，或者1。

• A: 1

• B: 011

• C: 010

• D: 00

这现在被称为赫夫曼编码，对于以下类型的例子，你无法超越它。继续尝试吧。

例如，如果你将D的编码缩短为0，那么一个消息011可能意味着DAA，或者可能只是B。因此，要使其工作，你需要引入字母间隔，这会抵消传输期间的任何节省。

那么，相比于原始的2,000位，这种压缩消息的效果如何？好吧，我们只需要计算平均每个字母的比特数。

因此，我们将每个编码的长度乘以出现概率，并将它们相加，这将导致平均每个符号1.75比特的长度。

$$1×0.5+3×0.125+3×0.125+2×0.25=1.75$$

这意味着通过赫夫曼编码，我们可以将消息从2,000位压缩到1,750位。

克劳德·香农是第一个声称`压缩极限将始终是消息源的熵`的人。

• 随着我们的源的熵或不确定性由于已知的统计结构而减少，压缩能力增加。（熵高，压缩能力差）

• 而如果熵由于不可预测性而增加，我们的压缩能力将减少。如果我们想要超越熵来进行压缩，我们必须在我们的消息中必然丢失信息。（熵低，压缩能力强）