出处: https://ocw.mit.edu/courses/6-050j-information-and-entropy-spring-2008/pages/bits-codes/翻译: ChatGPT

比特

信息是以比特为单位来度量的，就像长度以米为单位来度量，时间以秒为单位来度量一样。当然，知道信息的比特量并不等同于了解信息本身、其意义或其暗示。在这些笔记中，我们不会考虑信息的内容或意义，只考虑其数量。

在不同情况下需要不同的长度尺度。有时我们想以公里为单位测量长度，有时以英寸为单位，有时以$Ångströms$为单位。同样，除了比特之外，有时还使用其他信息尺度；在物理系统的上下文中，信息通常以焦耳每开尔文来度量。

Information is measured in bits, just as length is measured in meters and time is measured in seconds. Of course knowing the amount of information, in bits, is not the same as knowing the information itself, what it means, or what it implies. In these notes we will not consider the content or meaning of information, just the quantity.

Different scales of length are needed in different circumstances. Sometimes we want to measure length in kilometers, sometimes in inches, and sometimes in $Ångströms$. Similarly, other scales for information besides bits are sometimes used; in the context of physical systems information is often measured in Joules per Kelvin.

信息是如何量化的呢？考虑一种可能有几种不同结果的情况或实验。例子可能包括掷硬币（2种结果，正面或反面）或从一副扑克牌中选一张牌（52种可能的结果）。一个人（通常命名为Alice）如何简洁地告诉另一个人（Bob）此类实验或观察的结果？

How is information quantified? Consider a situation or experiment that could have any of several possible outcomes. Examples might be flipping a coin (2 outcomes, heads or tails) or selecting a card from a deck of playing cards (52 possible outcomes). How compactly could one person (by convention often named Alice) tell another person (Bob) the outcome of such an experiment or observation?

首先考虑掷硬币的两种结果，并假设它们是等可能的。如果Alice想告诉Bob硬币投掷的结果，她可以使用几种可能的技术，但它们在信息量上都是等价的，不论是说“正面”或“反面”还是说0或1。我们说，这样传递的信息是一个比特。

First consider the case of the two outcomes of flipping a coin, and let us suppose they are equally likely.If Alice wants to tell Bob the result of the coin toss, she could use several possible techniques, but they are all equivalent, in terms of the amount of information conveyed, to saying either "heads" or "tails" or to saying 0 or 1. We say that the information so conveyed is one bit.

如果Alice掷两次硬币，她可以通过说两次0或1来告诉四种可能结果中的哪一种。同样，八种等可能结果的实验结果可以用三比特来传达。

If Alice flipped two coins, she could say which of the four possible outcomes actually happened, by saying 0 or 1 twice. Similarly, the result of an experiment with eight equally likely outcomes could be conveyed with three bits,

更一般地，$2n$种结果可以用$n$比特来传达。因此，信息量是等可能结果数量的对数（以2为底）。

and more generally $2n$ outcomes with $n$ bits. Thus the amount of information is the logarithm (to the base 2) of the number of equally likely outcomes.

注意，传递信息需要两个阶段。首先是“设置”阶段，在此阶段，Alice和Bob就他们将要传达的内容以及每个比特序列的确切含义达成一致。这种共识称为编码。

Note that conveying information requires two phases. First is the "setup" phase, in which Alice and Bob agree on what they will communicate about, and exactly what each sequence of bits means. This common understanding is called the code.

例如，要传达从一副牌中选出的牌的花色，他们的编码可能是00表示梅花，01表示方块，10表示红心，11表示黑桃。编码的达成可以在任何观察发生之前进行，因此此时还没有信息需要传送。设置阶段可以包括通知接收者有新信息。

For example, to convey the suit of a card chosen from a deck, their code might be that 00 means clubs, 01 diamonds, 10 hearts, and 11 spades. Agreeing on the code may be done before any observations have been made, so there is not yet any information to be sent. The setup phase can include informing the recipient that there is new information.

然后是“结果”阶段，其中表示结果的实际0和1序列被发送。这些序列是数据。

Then, there is the "outcome" phase, where actual sequences of 0 and 1 representing the outcomes are sent. These sequences are the data.

使用约定的编码，Alice抽取牌，并通过发送两个比特的数据告诉Bob花色。她可以在多个实验中重复这样做，使用相同的编码。

Using the agreed-upon code, Alice draws the card, and tells Bob the suit by sending two bits of data. She could do so repeatedly for multiple experiments, using the same code.

在Bob知道抽取了一张牌但还未收到Alice的信息之前，他对花色是不确定的。他的不确定性或信息缺乏可以用比特来表示。听到结果后，他的不确定性会被接收到的信息所减少。在设置阶段，Bob的不确定性增加，然后在结果阶段减少。

After Bob knows that a card is drawn but before receiving Alice's message, he is uncertain about the suit.His uncertainty, or lack of information, can be expressed in bits. Upon hearing the result, his uncertainty is reduced by the information he receives. Bob's uncertainty rises during the setup phase and then is reduced during the outcome phase.

注意关于信息的一些重要事项，其中一些在此例中有所说明：

• 信息可以通过观察、实验或测量得知

• 信息是主观的，或“观察者相关的”。Alice知道的与Bob知道的不同（如果信息不是主观的，就没有必要进行交流）

• 在得知有观察可能有信息可用时，一个人的不确定性可能会增加，然后通过接收信息减少不确定性

• 信息可以丢失，无论是通过数据本身的丢失，还是通过编码的丢失

• 信息的物理形式是时空定位的。因此，

  • 信息可以从一个地方发送到另一个地方

  • 信息可以存储，然后在以后检索

Note some important things about information, some of which are illustrated in this example:

• Information can be learned through observation, experiment, or measurement

• Information is subjective, or "observer-dependent." What Alice knows is different from what Bob knows (if information were not subjective, there would be no need to communicate it)

• A person's uncertainty can be increased upon learning that there is an observation about which information may be available, and then can be reduced by receiving that information

• Information can be lost, either through loss of the data itself, or through loss of the code

• The physical form of information is localized in space and time. As a consequence,

  • Information can be sent from one place to another

  • Information can be stored and then retrieved later

1.1 布尔比特

如我们所见，信息可以通过0和1的序列进行传递。仅使用0和1，我们可以处理来自许多不同类型来源的数据，而无需关注数据的具体含义。因此，我们使用抽象的值，而不是具体的值。这种方法使我们能够忽略与特定信息处理和传输系统相关的许多复杂细节。

As we have seen, information can be communicated by sequences of 0 and 1 values. By using only 0 and 1, we can deal with data from many different types of sources, and not be concerned with what the data means. We are thereby using abstract, not specific, values. This approach lets us ignore many messy details associated with specific information processing and transmission systems.

比特很简单，只有两个可能的值。用于表示和操作单个比特的数学并不难。这种数学被称为布尔代数，以数学家乔治·布尔（George Boole，1815-1864）的名字命名。

Bits are simple, having only two possible values. The mathematics used to denote and manipulate single bits is not difficult. It is known as Boolean algebra, after the mathematician George Boole (1815–1864).

在某些方面，布尔代数类似于中学所教的整数或实数代数，但在其他方面有所不同。

In some ways Boolean algebra is similar to the algebra of integers or real numbers which is taught in high school, but in other ways it is different.

代数是数学的一个分支，处理具有某些可能值的变量，以及在给定一个或多个变量时返回具有某些可能值的结果的函数。对于布尔代数，可能的值是0和1。

Algebra is a branch of mathematics that deals with variables that have certain possible values, and with functions which, when presented with one or more variables, return a result which again has certain possible values. In the case of Boolean algebra, the possible values are 0 and 1.

首先考虑返回单个值的单变量布尔函数。它们共有四种。一个称为恒等（identity），仅返回其参数。另一个称为非（not，或否定、反转、补码），将0变为1，反之亦然。其他两个不管参数如何，只返回0或1。以下是这四个函数的表格：


注意，布尔代数比处理整数或实数的代数更简单，后者每个都有无穷多的单变量函数。

First consider Boolean functions of a single variable that return a single value. There are exactly four of them. One, called the identity, simply returns its argument. Another, called not (or negation, inversion, or complement) changes 0 into 1 and vice versa. The other two simply return either 0 or 1 regardless of the argument. Here is a table showing these four functions:

Note that Boolean algebra is simpler than algebra dealing with integers or real numbers, each of which has infinitely many functions of a single variable.

接下来，考虑具有两个输入变量A和B及一个输出值C的布尔函数。有多少种这样的函数呢？每个参数可以取两个值，因此有四种可能的输入模式（00、01、10和11）。将每个两变量布尔函数视为一个长度等于可能输入模式数量，即4的布尔值字符串。这样有且只有16（$24$）种不同的字符串组合，因此有且只有16种不同的两变量布尔函数。其中16种函数有两种完全忽略输入，四种将输出赋值为A或B或它们的补码，另外十种依赖于两个参数。最常用的有与（AND）、或（OR）、异或（XOR，exclusive or）、非与（NAND）和非或（NOR），如表1.2所示。（类似地，由于三输入布尔函数有8种可能的输入模式，因此有$28$或256种不同的三变量布尔函数。）


Next, consider Boolean functions with two input variables A and B and one output value C. How many are there? Each of the two arguments can take on either of two values, so there are four possible input patterns (00, 01, 10, and 11). Think of each Boolean function of two variables as a string of Boolean values 0 and 1 of length equal to the number of possible input patterns, i.e., 4. There are exactly 16 (24) different ways of composing such strings, and hence exactly 16 different Boolean functions of two variables. Of these 16, two simply ignore the input, four assign the output to be either A or B or their complement, and the other ten depend on both arguments. The most often used are AND, OR, XOR (exclusive or), *NAND* (not and), and NOR (not or), shown in Table 1.2. (In a similar way, because there are 8 possible input patterns for three-input Boolean functions, there are 28 or 256 different Boolean functions of three variables.)

人们往往倾向于将布尔值 0 和 1 视为整数 0 和 1。那么 AND 就相当于乘法，OR 则相当于加法，某种程度上是这样。然而，普通代数中的熟悉结果在布尔代数中并不成立，所以这种类比是危险的。重要的是要区分整数 0 和 1 与布尔值 0 和 1；它们不是同一个东西。

It is tempting to think of the Boolean values 0 and 1 as the integers 0 and 1. Then AND would correspond to multiplication and OR to addition, sort of. However, familiar results from ordinary algebra simply do not hold for Boolean algebra, so such analogies are dangerous. It is important to distinguish the integers 0 and 1 from the Boolean values 0 and 1; they are not the same.

布尔代数中有一种标准符号表示法。（这种表示法有时令人困惑，但其他不那么令人困惑的表示法在实践中很不方便。）AND 函数与乘法表示相同，通过将两个布尔值写在一起或在中间加一个点来表示：$A AND B$ 写作 $AB$ 或 $A⋅B$。OR 函数用加号表示：$A+B$ 意味着 $A OR B$。否定或 NOT 函数用符号或表达式上方的一条线表示，所以 $NOT A$ 是 $A$。最后，异或函数 XOR 用一个内部带加号的圆圈表示，$A⊕B$。


布尔代数还有其他可能的表示法。这里使用的是最常见的一种。有时，与（AND）、或（OR）和非（NOT）用 $AND(A,B)$、$OR(A,B)$ 和 $NOT(A)$ 的形式表示。有时使用中缀表示法，其中 $A∧B$ 表示 $A⋅B$，$A∨B$ 表示 $A+B$，$∼A$ 表示 $A$。在数学逻辑中，布尔代数也很有用，常用的表示法是 $A∧B$ 表示 $A⋅B$，$A∨B$ 表示 $A+B$，$¬A$ 表示 $A$。

There is a standard notation used in Boolean algebra. (This notation is sometimes confusing, but other notations that are less confusing are awkward in practice.) The AND function is represented the same way as multiplication, by writing two Boolean values next to each other or with a dot in between: $A AND B$ is written $AB$ or $A⋅B$. The OR function is written using the plus sign: $A+B$ means $A OR B$. Negation, or the NOT function, is denoted by a bar over the symbol or expression, so $NOT A$ is $A$. Finally, the exclusive-or function XOR is represented by a circle with a plus sign inside, $A⊕B$.

There are other possible notations for Boolean algebra. The one used here is the most common. Sometimes AND, OR, and NOT are represented in the form AND(A, B), OR(A, B), and NOT(A). Sometimes infix notation is used where A ∧ B denotes A · B, A ∨ B denotes A + B, and ∼A denotes A. Boolean algebra is also useful in mathematical logic, where the notation A ∧ B for A · B, A ∨ B for A + B, and ¬A for A is commonly used.

布尔函数的几个通用属性是有用的。可以通过简单地证明它们对所有可能的输入值都成立来证明这些属性。例如，如果知道输出值就能确定输入值，那么一个函数被称为可逆的。从这个意义上说，单变量的四个函数中有两个是可逆的（实际上是自逆的）。显然，两个（或更多）输入的函数本身都不可能是可逆的，因为输入变量比输出变量多。然而，如果结果组合的输出数量与输入数量相同，那么一些两个或更多这样的函数的组合可以是可逆的；例如，容易证明当通过返回第一个参数的函数增强时，异或函数 $A⊕B$ 是可逆的——更准确地说，具有两个输出的两变量函数，一个是 $A⊕B$，另一个是 $A$，是可逆的。

对于两变量函数，有许多属性需要考虑。例如，如果交换 $A$ 和 $B$ 时其值不变，即如果 $f(A,B)=f(B,A)$，则称一个两变量函数是交换的。因此，与（AND）函数是交换的，因为 $A⋅B=B⋅A$。其他15个函数中的一些也是交换的。布尔函数的其他一些属性在表1.4的恒等式中有所说明。


Several general properties of Boolean functions are useful. These can be proven by simply demonstrating that they hold for all possible input values. For example, a function is said to be reversible if, knowing the output, the input can be determined. Two of the four functions of a single variable are reversible in this sense (and in fact are self-inverse). Clearly none of the functions of two (or more) inputs can by themselves be reversible, since there are more input variables than output variables. However, some combinations of two or more such functions can be reversible if the resulting combination has the name number of outputs as inputs; for example it is easily demonstrated that the exclusive-or function $A⊕B$ is reversible when augmented by the function that returns the first argument—that is to say, more precisely, the function of two variables that has two outputs, one $A⊕B$and the other $A$, is reversible.

For functions of two variables, there are many properties to consider. For example, a function of two variables A and B is said to be commutative if its value is unchanged when $A$ and $B$ are interchanged, i.e.,if $f(A,B)=f(B,A)$. Thus the function AND is commutative because $A⋅B=B⋅A$. Some of the other 15 functions are also commutative. Some other properties of Boolean functions are illustrated in the identities in Table 1.4.

布尔位具有可以被复制（也可以被丢弃）的属性。在布尔代数中，复制是通过给位分配一个名称，然后多次使用该名称来完成的。由于这个属性，布尔位不是量子力学系统的良好模型。下面描述了一种不同的模型，量子位。

The Boolean bit has the property that it can be copied (and also that it can be discarded). In Boolean algebra copying is done by assigning a name to the bit and then using that name more than once. Because of this property the Boolean bit is not a good model for quantum-mechanical systems. A different model, the quantum bit, is described below.

1.2 电路位

组合逻辑电路是一种图形化表示布尔表达式的方法。每个布尔函数（NOT，AND，XOR 等）对应一个具有一个或两个输入和一个输出的“组合门”，如图 1.1 所示。不同类型的门具有不同的形状。线条用于将一个门的输出连接到一个或多个门的输入，如图 1.2 所示电路中所示。

逻辑电路广泛用于模拟数字电子电路，其中门代表集成电路的一部分，线条代表信号布线。

电路位可以被复制（通过将一个门的输出连接到两个或更多个门的输入）并且可以被丢弃（通过让一个输出未连接）。



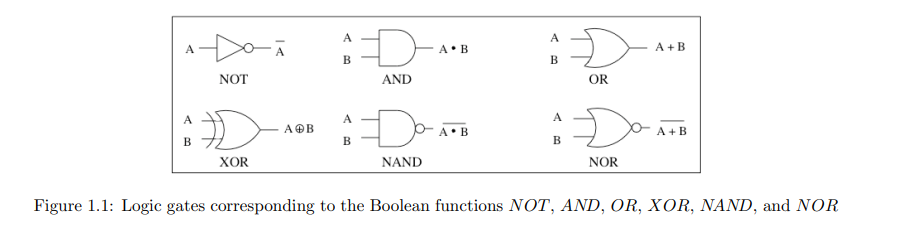
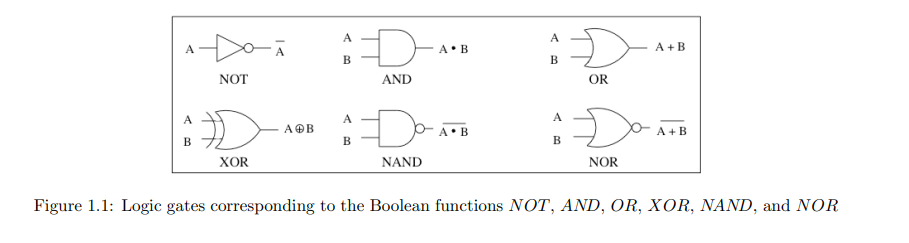
Combinational logic circuits are a way to represent Boolean expressions graphically. Each Boolean function (NOT, AND, XOR, etc.) corresponds to a "combinational gate" with one or two inputs and one output, as shown in Figure 1.1. The different types of gates have different shapes. Lines are used to connect the output of one gate to one or more gate inputs, as illustrated in the circuits of Figure 1.2.

Logic circuits are widely used to model digital electronic circuits, where the gates represent parts of an integrated circuit and the lines represent the signal wiring.

The circuit bit can be copied (by connecting the output of a gate to two or more gate inputs) and discarded (by leaving an output unconnected).

组合电路具有这样一种属性：一个门的输出永远不会反馈到任何其输出最终会馈送到第一个门输入的门的输入。换句话说，电路中没有环路。具有环路的电路称为时序逻辑，布尔代数不足以描述它们。

Combinational circuits have the property that the output from a gate is never fed back to the input of any gate whose output eventually feeds the input of the first gate. In other words, there are no loops in the circuit. Circuits with loops are known as sequential logic, and Boolean algebra is not sufficient to describe them.

例如，考虑图 1.3 中最简单的电路。反相器（NOT 门）将其输出连接到其输入。用布尔代数分析会导致矛盾。如果输入是 $1$，那么输出是 $0$，因此输入是 $0$。根据布尔代数的规则，不可能存在这种状态。另一方面，考虑图 1.3 中的两个反相器电路。该电路有两种可能的状态。如果底部电路有偶数个门，则有两个稳定状态；如果有奇数个门，则没有稳定状态。


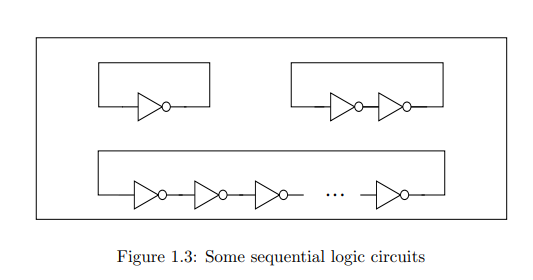
For example, consider the simplest circuit in Figure 1.3. The inverter (NOT gate) has its output connected to its input. Analysis by Boolean algebra leads to a contradiction. If the input is $1$ then the output is $0$ and therefore the input is $0$. There is no possible state according to the rules of Boolean algebra.On the other hand, consider the circuit in Figure 1.3 with two inverters. This circuit has two possible states. The bottom circuit has two stable states if it has an even number of gates, and no stable state if it has an odd number.

描述时序逻辑电路的行为需要比布尔代数更复杂的模型。例如，门或连接线（或两者）可以用时间延迟来建模。图 1.3 底部的电路（例如具有 13 个或 15 个门）通常称为环形振荡器，用于半导体工艺开发中测试使用新工艺制造的电路的速度。

A model more complicated than Boolean algebra is needed to describe the behavior of sequential logic circuits. For example, the gates or the connecting lines (or both) could be modeled with time delays. The circuit at the bottom of Figure 1.3 (for example with 13 or 15 gates) is commonly known as a ring oscillator, and is used in semiconductor process development to test the speed of circuits made using a new process.

1.3 控制位

在计算机程序中，布尔表达式通常用于确定控制流程，即执行哪些语句。例如，假设一个变量 $x$ 为负数而另一个变量 $y$ 为正数，那么第三个变量 $z$ 应该被设置为零。

In computer programs, Boolean expressions are often used to determine the flow of control, i.e., which statements are executed. Suppose, for example, that if one variable $x$ is negative and another $y$ is positive, then a third variable z should be set to zero.

在 Scheme 语言中，以下语句可以实现这一点：`(if (and (< x 0) (> y 0)) (define z 0))`（其他语言有自己的方式表达相同的意思）。

In the language Scheme, the following statement would accomplish this: `(if (and (< x 0) (> y 0)) (define z 0))` (other languages have their own ways of expressing the same thing).

控制位的代数类似于布尔代数，但有一个有趣的区别：任何不影响结果的控制表达式部分都可以忽略。在上述情况下（假设 and 的参数是从左到右求值的），如果 $x$ 被发现是正数，那么 $and$ 操作的结果是 $0$，无论 $y$ 的值如何，因此没有必要查看 $y$ 是否为正数，甚至不需要计算 $y$。结果是程序可以运行得更快，与 $y$ 计算相关的副作用也不会发生。

The algebra of control bits is like Boolean algebra with an interesting difference: any part of the control expression that does not affect the result may be ignored. In the case above (assuming the arguments of and are evaluated left to right), if $x$ is found to be positive then the result of the and operation is $0$ regardless of the value of $y$, so there is no need to see if $y$ is positive or even to evaluate y. As a result the program can run faster, and side effects associated with evaluating $y$ do not happen.

1.4 物理比特

如果要存储或传输比特，它必须具有物理形式。无论存储比特的对象是什么，它都有两个不同的状态，其中一个被解释为0，另一个被解释为1。通过将对象置于这两个状态之一来存储比特，当需要比特时，测量对象的状态。如果对象在不改变状态的情况下从一个位置移动到另一个位置，则发生了通信。如果对象在一段时间内保持在同一状态，则它作为存储器。如果对象的状态以随机方式改变，则其原始值已被遗忘。

If a bit is to be stored or transported, it must have a physical form. Whatever object stores the bit has two distinct states, one of which is interpreted as 0 and the other as 1. A bit is stored by putting the object in one of these states, and when the bit is needed the state of the object is measured. If the object has moved from one location to another without changing its state then communications has occurred. If the object has persisted over some time in its same state then it has served as a memory. If the object has had its state changed in a random way then its original value has been forgotten.

遵循工程学的基本要求（使其更小、更快、更强、更智能、更安全、更便宜），我们特别关注小型物理对象。一个对象能小到什么程度并且仍能存储一比特信息，其极限来源于量子力学。量子比特，或称量子位，是一种可以存储单个位的对象模型，但它非常小，以至于受制于量子力学对测量的限制。

In keeping with the Engineering Imperative (make it smaller, faster, stronger, smarter, safer, cheaper), we are especially interested in physical objects that are small. The limit to how small an object can be and still store a bit of information comes from quantum mechanics. The quantum bit, or qubit, is a model of an object that can store a single bit but is so small that it is subject to the limitations quantum mechanics places on measurements.

1.5 量子比特

根据量子力学，一个小物体可以有两个可测量的状态。这听起来非常适合存储比特，这种结果通常称为量子比特，发音为“cue-bit”。这两个值通常表示为 $∣0⟩$ 和 $∣1⟩$ 而不是 0 和 1，因为这种符号可以推广到表示多个量子比特所需的情况，并且避免了与实数 0 和 1 的混淆。量子力学有三个特性：可逆性、叠加和纠缠，使得量子比特或量子比特集合不同于布尔比特。

According to quantum mechanics, it is possible for a small object to have two states which can be measured. This sounds perfect for storing bits, and the result is often called a qubit, pronounced "cue-bit."
The two values are often denoted |0> and |1> rather than 0 and 1, because this notation generalizes to what is needed to represent more than one qubit, and it avoids confusion with the real numbers 0 and 1. There are three features of quantum mechanics, reversibility, superposition, and entanglement, that make qubits or collections of qubits different from Boolean bits.

**可逆性**：量子系统的一个特性是，如果一个状态可以通过某种转换转变为另一个状态，那么逆向转换也是可能的。因此，量子比特数学中的所有函数都是可逆的，函数的输出不能被丢弃，因为那将是不可逆的。然而，量子系统中至少有两个重要的不可逆性来源。首先，如果量子系统与环境相互作用且环境的状态未知，那么系统中的一些信息会丢失。其次，测量系统状态的行为本身就是不可逆的。

**Reversibility**: It is a property of quantum systems that if one state can lead to another by means of some transition, then the reverse transition is also possible. Thus all functions in the mathematics of qubits are reversible, and the output of a function cannot be discarded, since that would be irreversible. However, there are at least two important sources of irreversibility in quantum systems. First, if a quantum system interacts with its environment and the state of the environment is unknown, then some of the information in the system is lost. Second, the very act of measuring the state of a system is irreversible.

**叠加**：假设一个量子力学物体被准备成其两个状态的组合或叠加，即处于介于两种状态之间的某个状态。在这种情况下，测量的结果是什么呢？

在经典的非量子环境中，测量可以确定这种组合究竟是什么。此外，为了获得更高的精度，可以重复测量并对多个结果进行平均。然而，量子环境是不同的。在量子测量中，提出的问题是该物体是否处于某个特定状态，答案总是“是”或“否”，从来不是“也许”，也不是例如“27% 是，73% 否”。此外，测量后系统会处于与答案对应的状态，因此进一步的测量不会产生额外的信息。任何特定测量的结果是不可预测的，但答案的可能性可以用概率来表示。这种量子力学的特殊性质既限制了单个量子比特可以携带的信息量，同时也提供了设计利用这些特性的系统的机会。

**Superposition**: Suppose a quantum mechanical object is prepared so that it has a combination, or superposition, of its two states, i.e., a state somewhere between the two states. What is it that would be measured in that case?

In a classical, non-quantum context, a measurement could determine just what that combination is.Furthermore, for greater precision a measurement could be repeated, and multiple results averaged. However, the quantum context is different. In a quantum measurement, the question that is asked is whether the object is or is not in some particular state, and the answer is always either "yes" or "no," never "maybe" and never, for example, "27% yes, 73% no." Furthermore, after the measurement the system ends up in the state corresponding to the answer, so further measurements will not yield additional information. The result of any particular measurement cannot be predicted, but the likelihood of the answer, expressed in terms of probabilities, can. This peculiar nature of quantum mechanics offers both a limitation of how much information can be carried by a single qubit, and an opportunity to design systems which take special advantage of these features.

我们将通过一个例子来说明量子比特。让我们以光子作为我们的量子比特，光子是电磁辐射的基本粒子，包括无线电、电视和光。光子是从一个地方到另一个地方传递信息的良好候选者。它体积小，传输速度快。

光子的电场和磁场会同时振荡。电场的方向被称为偏振方向（在这里我们不考虑圆偏振光子）。因此，如果光子沿 $z$ 方向传播，其电场可以在 $x$ 方向、$y$ 方向，或者实际上在 $x−y$ 平面的任何方向振荡，有时称为“水平-垂直平面”。

偏振可以用来存储一位信息。因此，如果比特是 $∣0⟩$，Alice 可以准备一个具有水平偏振的光子；如果比特是 $∣1⟩$，则准备一个具有垂直偏振的光子。当 Bob 得到光子时，他可以测量其垂直偏振（即询问偏振是否为垂直）。如果答案是“是”，那么他推断比特是 $∣1⟩$。

有人可能认为，单个光子的偏振可以传输不止一位信息。为什么 Alice 不能使用不同于水平和垂直的偏振角度来发送两位信息呢？为什么不使用水平、垂直、向右倾斜的中间位置和向左倾斜的中间位置？问题在于 Bob 必须决定测量的角度。由于量子力学的限制，他不能问“偏振角度是多少”这个问题，而只能问“偏振是否在我选择的方向”。他的测量结果只能是“是”或“否”，换句话说，只能得到一位信息。而且在测量之后，光子会处于他测量的平面（如果结果是“是”）或者垂直于该平面的平面（如果结果是“否”）。

如果 Bob 想更准确地测量偏振角度，为什么不能多次重复测量并取平均值呢？这是行不通的，因为第一次测量的行为会将偏振角度重置为他测量的角度或垂直于该角度的方向。因此，后续的测量结果都将相同。

或者，Bob 可能决定制作光子的多个副本，然后对每个副本进行测量。这种方法也行不通。他唯一可以复制光子的方法是测量其属性，然后创建一个具有完全相同属性的新光子。他创建的所有光子都将是相同的。

如果 Alice 以任意角度准备了光子，Bob 会测量到什么？或者如果光子的偏振角度因为沿途的随机相互作用而发生了变化？或者如果光子被恶意窃听者（通常称为 Eve）以某个角度测量并因此重置为该角度？在这些情况下，无论 Bob 选择测量哪个偏振方向，他总会得到“是”或“否”的答案，实际偏振越接近测量方向，答案是“是”的可能性越大。具体来说，答案是“是”的概率是 Bob 的测量角度与 Alice 的准备角度之间角度余弦的平方。无法预测 Bob 任何一次测量的结果。这种固有的随机性是量子力学的不可避免的方面。

We will illustrate quantum bits with an example. Let's take as our qubit a photon, which is the elementary particle for electromagnetic radiation, including radio, TV, and light. A photon is a good candidate for carrying information from one place to another. It is small, and travels fast.

A photon has electric and magnetic fields oscillating simultaneously. The direction of the electric field is called the direction of polarization (we will not consider circularly polarized photons here). Thus if a photon is headed in the z-direction, its electric field can be in the x-direction, in the y-direction, or in fact in any direction in the x-y plane, sometimes called the "horizontal-vertical plane."
The polarization can be used to store a bit of information. Thus Alice could prepare a photon with horizontal polarization if the bit is $∣0⟩$ and vertical polarization if the bit is $∣1⟩$. Then when Bob gets the photon, he can measure its vertical polarization (i.e., ask whether the polarization is vertical). If the answer is "yes," then he infers the bit is $∣1⟩$.

It might be thought that more than a single bit of information could be transmitted by a single photon's polarization. Why couldn't Alice send two bits, using angles of polarization different from horizontal and vertical? Why not use horizontal, vertical, half-way between them tilted right, and half-way between them tilted left? The problem is that Bob has to decide what angle to measure. He cannot, because of quantummechanical limitations, ask the question "what is the angle of polarization" but only "is the polarization in the direction I choose to measure." And the result of his measurement can only be "yes" or "no," in other words, a single bit. And then after the measurement the photon ends up either in the plane he measured (if the result was "yes") or perpendicular to it (if the result was "no").

If Bob wants to measure the angle of polarization more accurately, why couldn't he repeat his measurement many times and take an average? This does not work because the very act of doing the first measurement resets the angle of polarization either to the angle he measured or to the angle perpendicular to it. Thus subsequent measurements will all be the same.

Or Bob might decide to make multiple copies of the photon, and then measure each of them. This approach does not work either. The only way he can make a copy of the photon is by measuring its properties and then creating a new photon with exactly those properties. All the photons he creates will be the same.

What does Bob measure if Alice had prepared the photon with an arbitrary angle? Or if the photon had its angle of polarization changed because of random interactions along the way? Or if the photon had been measured by an evil eavesdropper (typically named Eve) at some other angle and therefore been reset to that angle? In these cases, Bob always gets an answer "yes" or "no," for whatever direction of polarization he chooses to measure, and the closer the actual polarization is to that direction the more likely the answer is yes. To be specific, the probability of the answer yes is the square of the cosine of the angle between Bob's angle of measurement and Alice's angle of preparation. It is not possible to predict the result of any one of Bob's measurements. This inherent randomness is an unavoidable aspect of quantum mechanics.

**纠缠**：两个或多个量子比特可以以特定的方式一起准备。其中一个属性，我们现在不再进一步讨论，称为“纠缠”。例如，两光子可能具有相同的偏振（要么都是水平的，要么都是垂直的）。然后它们可能前往不同的地方，但保持其纠缠的偏振。它们在物理位置上是分开的，但在偏振上不是。如果你将它们视为两个独立的光子，可能会想为什么一个光子的偏振测量会影响另一个位于远处的光子的后续测量。

请注意，量子系统并不总是表现出与叠加和纠缠相关的特殊性。例如，光子可以独立地被准备（所以没有纠缠），偏振角度可以被限制为水平和垂直（没有叠加）。在这种情况下，量子比特的行为就像布尔比特。

**Entanglement**: Two or more qubits can be prepared together in particular ways. One property, which we will not discuss further now, is known as "entanglement." Two photons, for example, might have identical polarizations (either both horizontal or both vertical). Then they might travel to different places but retain their entangled polarizations. They then would be separate in their physical locations but not separate in their polarizations. If you think of them as two separate photons you might wonder why measurement of the polarization of one would affect a subsequent measurement of the polarization of the other, located far away.

Note that quantum systems don't *always* exhibit the peculiarities associated with superposition and entanglement. For example, photons can be prepared independently (so there is no entanglement) and the angles of polarization can be constrained to be horizontal and vertical (no superposition). In this case qubits behave like Boolean bits.

1.5.1 量子比特的优势

在量子环境中可以完成一些经典环境下无法完成的事情，其中一些是有利的。

There are things that can be done in a quantum context but not classically. Some are advantageous.

这里有一个例子：
再次考虑 Alice 试图使用偏振光子向 Bob 发送信息。她准备了具有水平或垂直偏振的光子，并在设置阶段告诉 Bob。现在假设破坏者 Sam 想通过在 Alice 和 Bob 之间的某个路径点处理光子来破坏这次通信。他使用一台机器以他选择的角度测量偏振。如果他选择 $45∘$，每个光子的偏振最终将是该角度或垂直于该角度，无论其原始偏振是什么。然后 Bob 进行垂直测量时，不论 Alice 发送了什么，他的测量结果将一半为 $0$，一半为 $1$。

Alice 得知了 Sam 的计划，想要重新建立与 Bob 的可靠通信。她能做些什么呢？

她通过 Sam 无法窃听的路径告诉 Bob，她将发送 $45∘$ 和 $135∘$ 的光子，因此他应该在这些角度之一进行测量。这样 Sam 的机器就不会改变光子的偏振。当然，如果 Sam 发现 Alice 的做法，他可以将他的机器旋转回垂直角度。或者，其他的对策和反制措施也可以采取。

这个情景依赖于光子的量子特性，以及单个光子除了沿特定偏振角度外不能被 Sam 测量的事实。因此，Alice 用于挫败 Sam 的技术在经典比特中是不可能实现的。

Here is one example:
Consider again Alice trying to send information to Bob using polarized photons. She prepares photons that have either horizontal or vertical polarization, and tells that to Bob, during the setup phase. Now let us suppose that a saboteur Sam wants to spoil this communication by processing the photons at some point in the path between Alice and Bob. He uses a machine that simply measures the polarization at an angle he selects. If he selects $45◦$, every photon ends up with a polarization at that angle or perpendicular to it, regardless of its original polarization. Then Bob, making a vertical measurement, will measure $0$ half the time and $1$ half the time, regardless of what Alice sent.

Alice learns about Sam's scheme and wants to reestablish reliable communication with Bob. What can she do?

She tells Bob (using a path that Sam does not overhear) she will send photons at $45◦$ and $135◦$, so he should measure at one of those angles. Sam's machine then does not alter the photons. Of course if Sam discovers what Alice is doing, he can rotate his machine back to vertical. Or there are other measures and counter-measures that could be put into action.

This scenario relies on the quantum nature of the photons, and the fact that single photons cannot be measured by Sam except along particular angles of polarization. Thus Alice's technique for thwarting Sam is not possible with classical bits.

1.6 经典比特

由于量子测量通常会改变被测量的对象，量子比特不能被二次测量。另一方面，如果一个比特由具有相同属性的多个对象表示，那么在测量后，仍有足够的对象保持不变，从而可以再次测量相同的比特。

Because quantum measurement generally alters the object being measured, a quantum bit cannot be measured a second time. On the other hand, if a bit is represented by many objects with the same properties, then after a measurement enough objects can be left unchanged so that the same bit can be measured again.

在当今的电子系统中，一位信息由许多对象携带，所有这些对象都以相同的方式准备（或者至少这是一个方便的看法）。因此，在半导体存储器中，一个比特是由大约 60,000 个电子的存在或不存在表示的（这些电子储存在一个充电到 $1V$ 的 $10fF$ 电容上）。同样，在无线电通信中也使用大量光子。

In today's electronic systems, a bit of information is carried by many objects, all prepared in the same way (or at least that is a convenient way to look at it). Thus in a semiconductor memory a single bit is represented by the presence or absence of perhaps 60,000 electrons (stored on a $10fF$ capacitor charged to $1V$ ). Similarly, a large number of photons are used in radio communication.

由于涉及许多对象，对它们的测量不限于简单的“是”或“否”，而是可以在连续值范围内变化。因此，半导体逻辑元件上的电压可能在 $0V$ 到 $1V$ 的范围内的任何地方。电压可能会被解释为允许误差范围，因此 $0V$ 到 $0.2V$ 之间的电压表示逻辑 $0$，而 $0.8V$ 到 $1V$ 之间的电压表示逻辑 $1$。电路不保证正确解释 $0.2V$ 和 $0.8V$ 之间的电压。如果电路中的噪声始终小于 $0.2V$，并且每个电路门的输出要么是 $0V$，要么是 $1V$，那么这些电压始终可以无误地解释为比特。

这种电路显示出所谓的“恢复逻辑”，因为在信息处理过程中，电压从理想值 $0V$ 和 $1V$ 的小偏差被消除。现代计算机的稳健性依赖于恢复逻辑的使用。

Because many objects are involved, measurements on them are not restricted to a simple yes or no, but instead can range over a continuum of values. Thus the voltage on a semiconductor logic element might be anywhere in a range from, say, $0V$ to $1V$ . The voltage might be interpreted to allow a margin of error, so that voltages between $0V$ and $0.2V$ would represent logical $0$, and voltages between $0.8V$ and $1V$ a logical $1$. The circuitry would not guarantee to interpret voltages between $0.2V$ and $0.8V$ properly. If the noise in a circuit is always smaller than $0.2V$ , and the output of every circuit gate is either $0V$ or $1V$ , then the voltages can always be interpreted as bits without error.

Circuits of this sort display what is known as "restoring logic" since small deviations in voltage from the ideal values of $0V$ and $1V$ are eliminated as the information is processed. The robustness of modern computers depends on the use of restoring logic.

经典比特是一种抽象模型，其中比特可以在不扰动的情况下被测量。因此，可以复制经典比特。对于使用恢复逻辑的电路，这种模型非常适用。

A classical bit is an abstraction in which the bit can be measured without perturbing it. As a result copies of a classical bit can be made. This model works well for circuits using restoring logic.

由于所有物理系统最终都遵循量子力学，经典比特始终是现实的近似。然而，即使使用最现代化、最小的设备，它也是一个极好的近似。

Because all physical systems ultimately obey quantum mechanics, the classical bit is always an approximation to reality. However, even with the most modern, smallest devices available, it is an excellent one.

一个有趣的问题是，随着半导体技术的进步使元件尺寸减小，经典比特的近似是否会继续有用。最终，当我们尝试用少量原子或光子来表示或控制比特时，量子力学的限制作用将变得重要。难以准确预测何时会发生这种情况，但一些人认为这会在 2015 年之前发生。

An interesting question is whether the classical bit approximation will continue to be useful as advances in semiconductor technology allow the size of components to be reduced. Ultimately, as we try to represent or control bits with a small number of atoms or photons, the limiting role of quantum mechanics will become important. It is difficult to predict exactly when this will happen, but some people believe it will be before the year 2015.

1.7 总结

在不同的上下文中，比特有几种不同的模型。这些模型并不完全相同。在本文的其余部分中，布尔比特将最常使用，但有时也需要用到量子比特。

There are several models of a bit, useful in different contexts. These models are not all the same. In the rest of these notes, the Boolean bit will be used most often, but sometimes the quantum bit will be needed.

引用声明

MIT OpenCourseWare http://ocw.mit.edu

关于引用这些材料或我们的使用条款的信息，请访问：[http://ocw.mit.edu/terms](http://ocw.mit.edu/terms)。

For information about citing these materials or our Terms of Use, visit: http://ocw.mit.edu/terms.