原始观点

【Reed-Solomon 擦除码 Python 实现：二 (甲) 范德蒙矩阵】 https://www.bilibili.com/video/BV1ue411B75E/?share_source=copy_web&vd_source=04259c9260832797bf08914e26e438d5

范德蒙矩阵


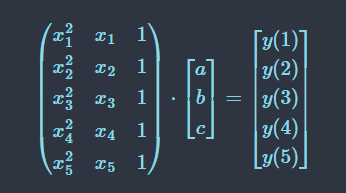
$y=pm​(x)$中，x 预先约定，message 控制多项式 $pm​$ 的系数，实际传输的是 y 值。

Encoding: polynomial evaluation, matrix-vector multiplication
Erasure Decoding: solve linear equations

Shannon's Birthday date as polynomial coefficients

Message: 6 digits of the date are [d0, d1, d2, ..., d5], let's make a polynomial of degree 5 using those coefficients:$c(x)=d0​+d1​x+d2​x2+⋯+d5​x5$

Codeword of 9 values: [c(0), c(1), c(2), ... c(8)]

Shannon's Birthday using Vandermonde matrix：

$d=(d0​,d1​,…,d5​)T,c=(c0​,c1​,…,c8​)T$


$V⋅d=c$

假设 c0, c4, c8 丢失，我们用剩下的数据列线性方程组。


解出 d = [1, 6, 0, 4, 3, 0], 故 Shannon 的生日是 1916-04-30。

多项式编码的基本原理是这样，实际上还有一些困难需要克服，才能投入使用

• 消息长度 k = 多项式次数 + 1，codeword 长度为 n，如何保证任选 k 行始终有解

• 编码不用大整数 $(n−1)k−1$，解码不用浮点数。

• codeword symbol 的取值范围最好和 message symbol [d0, d1, ...] 一样，都是字节 [0, 255]。这就要用 Finite Field，也叫 Galois Field 迦罗华域。

• 如何在没有传丢数据的情况下跳过解码步骤

  • systematic code: [c0, c1, ..., c5, c6, c7, c8] = [d0, d1, ... d5, p0, p1, p2]

系统码

如果 d0.. d5 中没有丢失(erasure)，那么无需解码。

$$An×k​=[Ik​G​]⋅d=[dc​]$$Generator matrix $G(n−k)×k​$ for parity.$d=[d0​,d1​,d2​,…,dk​]$$c=[c0​,c1​,…,cn−k​]$

运用消元法，将范德蒙矩阵进行消元便可得到该矩阵：



或者，通过逆运算

Sysieniatic enciding using inverse of Vandermonde matrix


也可通过列变换：



解码

Systematic encoding


如果 $d0​…d5​$ 中没有丢失(erosure)，那么无需解码。
纠错能力

• 假如 $d0​…d5​$ 中丢失任何一个，那么只要知道 $c0​,c1​,c2​$ 中的任何一个就能恢复。

• 假如 $d0​…d5​$ 中丢失任何两个，那么只要知道 $c0​,c1​,c2​$ 中的任何两个就能恢复。

• 假如 $d0​…d5​$ 中丢失任何三个，那么要知道 $c0​,c1​,c2​$ 才能恢复。
  注意是丢失，不是传错，这是 erasure code 区别于 error correction code 的地方。

假设丢失了 $d5​$，如何从 $d0​...d4​$, $c0​$ 恢复 $d5​$ ？


对左边的矩阵求逆


假设丢失了 $d2​,d3​,d5​$，如何从 $d0​...d4​$, $c0​,c1​,c2​$ 恢复原始数据？


如法炮制


要求：$An×k​$ 的任意 $k$ 行都是可逆的。


Send [1, 1, 4, 5, 1, 4, 10, 14, 12]
Got [1, 1, ?, ?, 1, 4, 10, 14]