纠错码-学习笔记
纠错
纠错基础
算法概述
参考内容如下:
NAND Error Correction Codes Introduction https://www.macronix.com/Lists/ApplicationNote/Attachments/1910/AN0271V1-NAND%20Error%20Correction%20Codes%20Introduction-0217.pdf
Error Correction Codes in NAND Flash Memory https://repositories.lib.utexas.edu/server/api/core/bitstreams/b6236ec2-8df3-4be9-93ca-2c7a52912d31/content
Error Correcting Codes https://youtu.be/eixCGqdlGxQ?si=_lnfKISRmoAGXiRf
由于 NAND 闪存中的数据在存储或读取过程中可能因物理干扰而发生错误,因此必须引入纠错机制(ECC)以确保数据的完整性。除此之外,纠错码在其它领域也有广泛应用,例如:
卫星通信:Reed-Solomon 码最早便应用于航天通信。太空中存在强烈的电磁辐射和宇宙射线,极易导致数据传输错误,而 Reed-Solomon 码能有效纠正突发错误,保障通信可靠性。
二维码(QR Code):采用 BCH 码进行纠错。二维码通过黑白模块分别表示二进制的 0 和 1,但在实际使用中可能因污损、遮挡或打印缺陷而造成信息丢失,纠错机制可确保即使部分图案受损,原始信息仍能被准确恢复。
无线通信设备(如5G):现代通信系统广泛采用 LDPC(低密度奇偶校验)码。在网络传输过程中,信号易受噪声、多径效应等干扰,LDPC 码凭借接近香农极限的性能,显著提升了数据传输的鲁棒性与效率。
纠错算法主要有Hamming、Reed-Solomon、BCH、LDPC:

其中, Error types 中,Reed-Solomon 优点在于处理 Burst Errors 的原因可见下图:
通信模型
在数字通信或存储系统中,为了在噪声或干扰环境下可靠地传输或保存信息,通常采用信道编码(即纠错编码)技术。其基本通信模型包含以下几个核心环节:
原始消息(Message)
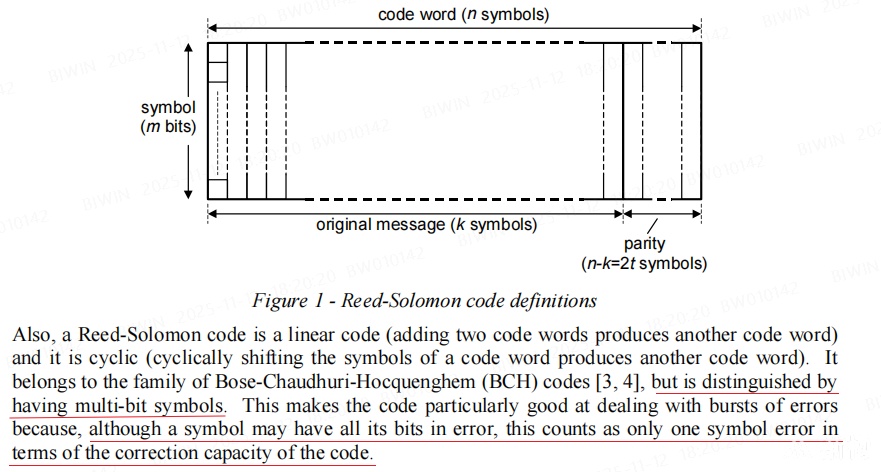
发送端希望传输的信息,通常表示为一个长度为 k 的二进制序列 m=(m1,m2,\dots,mk)。这是用户数据本身,尚未加入任何冗余。编码与码字(Codeword)
编码器将原始消息 m 按照特定的纠错码规则(如 Hamming 码、BCH 码、LDPC 等)进行处理,生成一个更长的二进制序列——码字(Codeword),记为 c=(c1,c2,\dots,cn),其中 n>k。
码字由两部分组成:信息位:即原始消息本身;
校验位(Parity Bits):额外添加的冗余比特,用于检测和纠正错误。校验位的数量为 r=n−k,其值由信息位通过特定代数关系(如线性方程、多项式运算等)计算得出。
信道传输与接收(Received Word)
码字 c 经过物理信道(如无线链路、NAND 闪存、光纤等)传输后,可能因噪声、干扰或器件老化而发生比特翻转,接收端收到的是一个可能含错的序列 r=(r1,r2,\dots,rn),称为接收字(Received Word)。解码与纠错
接收端的解码器利用码字中内嵌的冗余结构(即校验位提供的约束关系)对 r 进行分析,判断是否出错,并尽可能恢复出原始的码字 c,最终提取出正确的消息 m。
例如,Nand 一个 page 总共有18k 数据,其中16k 是 原始信息,2k是校验位,这18k数据为码字。由于 retention、disturb 等应力出现 bit 翻转,读取时得到的数据为接收字,如果翻转个数在算法纠错范围以内,那么,经过解码后就可得到原始信息,否则解码失败。
以最简单的重复码(Repetition Code)为例,顺便对比三个概念:检错、纠删和纠错。
假设原始消息为:M=1100
检错(Error Detection)
编码:将消息重复两次,得到码字
C=1100 1100接收:信道中第 2 位发生翻转(1 → 0),接收端收到
R=1000 1100分析:接收端对比两份副本,发现第 2 位不一致(0 vs 1),可以确定发生了错误。
局限:但无法判断哪一份是正确的——是第一份的第 2 位错了,还是第二份错了?因此只能检测错误,不能纠正。
纠删(Erasure Correction)
编码:同样使用重复两次的码字
C=1100 1100接收:第 2 位因遮挡、污损等原因完全丢失(例如二维码部分被涂黑),接收端知道该位置“不可靠”,记为擦除符号
_:
R=1_00 1100分析:由于接收端明确知道第 2 位缺失(即“擦除位置”已知),只需参考另一副本即可恢复:第二份副本中第 2 位是
1,因此可确定原值为1。优势:纠删比纠错更容易,因为错误位置已知,只需填补缺失值。
纠错(Error Correction)
编码:为提升容错能力,将消息重复三次
C=1100 1100 1100接收:第 2 位在第一份副本中翻转(1 → 0),其余正确:
R=1000 1100 1100分析:接收端对每一位进行多数表决(Majority Voting):
第 1 位:1, 1, 1 → 1
第 2 位:0, 1, 1 → 1(多数)
第 3 位:0, 0, 0 → 0
第 4 位:0, 0, 0 → 0
因此恢复出原始消息1100。
前提:假设信道最多只发生 1 次比特翻转(即错误数 ≤ 1),则重复三次可可靠纠正单比特错误。
总结:
类型 | 是否知道错误位置 | 能否恢复原始数据 | 所需冗余 | 典型应用 |
|---|---|---|---|---|
检错 | ❌ 否 | ❌ 仅能发现错误 | 低 | 网络协议校验、内存奇偶校验 |
纠删 | ✅ 是(已知擦除位置) | ✅ 可恢复 | 中 | 二维码、CD/DVD 刮痕恢复 |
纠错 | ❌ 否 | ✅ 可恢复(在错误数限制内) | 高 | 卫星通信、SSD 存储、5G |
重复编码类比:假设在山上信号差,发送消息会有丢失的风险,那么可试下同一条消息多发几次,只要对方收到一次,就能得到发送源的消息。
以经典的 (7,4) 汉明码 为例:
阶段 | 内容 | 说明 |
|---|---|---|
Message |
| 原始 4 位用户数据 |
Codeword |
| 添加 3 个校验位后的 7 位合法码字 |
Received |
| 传输中第 3 位出错 |
Corrected |
| 通过汉明码检测并纠正单比特错误 |
Reed-Solomon python代码示例:
from reedsolo import RSCodec
import random
# ========== 用户可配置参数 ==========
MESSAGE = b'hello' # 原始消息
NSYM = 4 # 校验 symbol 数量(每个 symbol = 1 字节 = 8 bits)
NUM_ERRORS_TO_SIMULATE = 2 # 模拟出错的 symbol 数量(应 ≤ NSYM // 2 才能可靠纠正)
# ===================================
MAX_CORRECTABLE = NSYM // 2 # Reed-Solomon 最多可纠正的 symbol 数量
def bytes_to_binary_str(data: bytes) -> str:
"""将字节序列转为连续的二进制字符串(每字节8位)"""
return ''.join(f'{b:08b}' for b in data)
def print_bytes_with_symbols(data: bytes, label: str):
"""打印字节数据,并标注每个字节是一个 symbol"""
print(f"\n{label}:")
print("Symbols (each = 8 bits / 1 byte):")
for i, byte in enumerate(data):
print(f" Symbol[{i:2d}] = 0x{byte:02X} = {byte:08b}")
print("Full binary string:")
print(" " + bytes_to_binary_str(data))
# 1. 原始消息
print("原始消息:", MESSAGE.decode())
print(f"消息长度: {len(MESSAGE)} symbols (bytes)")
print_bytes_with_symbols(MESSAGE, "1. 原始消息 (symbols)")
# 2. Reed-Solomon 编码
print(f"\n使用 Reed-Solomon 编码:")
print(f" - 校验 symbol 数 (nsym): {NSYM}")
print(f" - 最大可纠正 symbol 数: {MAX_CORRECTABLE}")
rsc = RSCodec(nsym=NSYM)
encoded = rsc.encode(MESSAGE)
print(f"编码后总长度: {len(encoded)} symbols ({len(MESSAGE)} data + {NSYM} parity)")
print_bytes_with_symbols(encoded, "2. 编码后数据 (data + parity symbols)")
# 3. 模拟 symbol 级错误
if NUM_ERRORS_TO_SIMULATE > len(encoded):
raise ValueError("模拟错误数不能超过编码后总长度")
corrupted = bytearray(encoded)
error_positions = random.sample(range(len(corrupted)), NUM_ERRORS_TO_SIMULATE)
for pos in error_positions:
corrupted[pos] ^= 0xFF # 破坏整个 symbol(8 bits)
print(f"\n3. 模拟 {NUM_ERRORS_TO_SIMULATE} 个 symbol 错误 "
f"({'✓ 在可纠正范围内' if NUM_ERRORS_TO_SIMULATE <= MAX_CORRECTABLE else '✗ 超出纠错能力'})")
print("Error positions (symbol indices):", sorted(error_positions))
print_bytes_with_symbols(corrupted, "出错后的数据")
# 4. 解码并纠错
try:
decoded_message, decoded_msgecc, errata_pos = rsc.decode(corrupted)
print("\n4. ✅ 解码成功!")
print("恢复的消息:", decoded_message.decode())
print("成功纠正的 symbol 位置:", sorted(errata_pos))
print(f"注意:Reed-Solomon 按 symbol(8-bit)单位纠错,最多可纠 {MAX_CORRECTABLE} 个 symbol 错误。")
except Exception as e:
print("\n4. ❌ 解码失败:", e)
print(f"原因:错误 symbol 数 ({NUM_ERRORS_TO_SIMULATE}) 超过最大可纠正数 ({MAX_CORRECTABLE})")纠错本质
纠错的过程是,当我们接受到无效编码(invalid code)时,解码的过程就是找到其最近的有效编码(valid code)。
"Best 2 out of 3" Repetition Code 是将信息从一维变换成三维:
0 -> 000
1 -> 111
在这个三维空间中,000 和 111 被视为有效编码,其它如:001, 100, 010, 101, 110, 011等则视为无效编码。当接受到的信息是这些无效编码时,可认为是传输过程中出现了比特翻转。
例如,当接受到 001 时,最近的有效编码是 000;接受到 110 时,最近的有效编码是 111。

"Hamming (7,4) Code" (可纠错 1bit 错误)是将信息从四维变换成七维,例如,
0010 -> 0010011
1100 -> 1100011
在这个七维空间中,有 128 (27) 个 codewords,其中仅有16 (24)个是有效编码(valid code),下表蓝色高亮的部分为有效编码。

七维空间的可视化如下图,右侧的红点表示的是有效编码:

详细内容见: https://en.wikiversity.org/wiki/Reed%E2%80%93Solomon_codes_for_coders#BCH_codes
简要来说,采用下面python代码,message = 00011 (十进制为3),会被编码成 codeword = 000111101011001
编码代码:
def qr_check_format(fmt):
g = 0x537 # = 0b10100110111 in python
for i in range(4,-1,-1):
if fmt & (1 << (i+10)):
fmt ^= g << i
return fmt
format = 0b00011
encoded_format = (format<<10) + qr_check_format(format<<10)由于原始消息长度为 5 比特,因此合法码字(valid codeword)仅有 25=32 个。在这种小规模码空间下,可以通过暴力枚举所有合法码字,并计算其与接收序列之间的汉明距离,从而实现最大似然译码(即选择距离最小的码字作为估计结果)。
解码代码:
def hamming_weight(x):
weight = 0
while x > 0:
weight += x & 1
x >>= 1
return weight
def qr_decode_format(fmt):
best_fmt = -1
best_dist = 15
for test_fmt in range(0,32):
test_code = (test_fmt<<10) ^ qr_check_format(test_fmt<<10)
test_dist = hamming_weight(fmt ^ test_code)
if test_dist < best_dist:
best_dist = test_dist
best_fmt = test_fmt
elif test_dist == best_dist:
best_fmt = -1
return best_fmt实测情况如下:
>>> from qr import *
>>> qr_decode_format(int("000111101011001",2)) # no errors
3
>>> qr_decode_format(int("111111101011001",2)) # 3 bit-errors
3
>>> qr_decode_format(int("111011101011001",2)) # 4 bit-errors
-1结果表明:当错误位数不超过 3 时,可成功纠正;一旦达到 4 位错误,则无法可靠恢复。
其根本原因在于唯一最近邻性:
在前两种情况下,接收序列与某个合法码字的距离严格小于与其他所有码字的距离,因此可唯一确定原始消息;
而在第三种情况中,接收序列
111011101011001与至少两个不同的合法码字具有相同的最小汉明距离(例如均为 4),导致译码器无法判断哪一个才是真正的发送码字,故返回-1表示“不可纠”。
以该接收序列为具体例子,存在如下两个等距的合法码字:
111011101011001 (接受到的码字)
000111101011001 (message = 00011,希望还原到的)
111010110010001 (message = 11101)
两者与接收序列 111011101011001 的汉明距离相同,因此译码结果不唯一。
这也揭示了纠错码的一个基本限制:纠错能力取决于码字之间的最小距离。QR 码格式信息采用的 (15,5) BCH 码最小距离为 7,理论上最多可纠正 (7−1)/2=3 bits 错误——与上述实验结果完全一致。
纠错能力
衡量纠错能力需要几个概念: 汉明权重、汉明距离、最小汉明距离
Hamming Weight w(⋅)
The number of non-zero digits in a codeword(# of 1s)
w(00110)=2,w(111)=3,w(0001)=1
Hamming Distance D(⋅,⋅)
The number of digits where two codewords differ
D(000,111)=3,3个bit都不同
D(00110,00111)=1,第 5 个 bit 不同
D(0000,1001)=2,第 1 和第 4 个 bit 不同
D(c,00000)=w(c),上面说过汉明权重 w(c) 是 codeword 中所有非 0 的个数
Minimum Distance d
Smallest Hamming distance between any two (valid) codewords
"Best 2 out of 3" Repetition Code
Generator Matrix:[1 1 1]
Message | Codeword |
|---|---|
0 | 000 |
1 | 111 |
"Best 2 out of 3" Repetition Code 只有 000 和 111,则其最小汉明距离是 3。
the Minimum Distance of a code tells us how many error bits we are guaranteed to fix.

重复次数 | c1 | c2 | Distance | # errors detected | # errors corrected |
|---|---|---|---|---|---|
1 | 0 | 1 | 1 | 0 | 0 |
2 | 00 | 11 | 2 | 1 | 0 |
3 | 000 | 111 | 3 | 2 | 1 |
4 | 0000 | 1111 | 4 | 3 | 1 |
5 | 00000 | 11111 | 5 | 4 | 2 |
以重复次数为4为例,如果
翻转 3 bits,如 0000 翻转成 1011,可以判断出了错,但无法纠回 0000,只会错误纠成 1111
翻转 2 bits,如 0000 翻转成 1001,可以判断出了错,依然无法纠回 0000
翻转 1 bits,如 0000 翻转成 1000,可以判断出了错,可纠回 0000
通过排列组合不同 valid codeword 来找 Minimum Distance 计算量过大,可以转换成其它方式来找。
this won't change the end resulting distance that we get since by subtracting a code word we're basically just sliding valid codewords over in space without changing the distance between them.
又因为:
Sum of any two valid codewords is another valid codeword,
D(c,00000)=w(c)
所以:
so the minimum distance is just equal to the smallest nonzero Hamming weight over all valid codewords in the code: d=c⃗minw(c⃗)
"Hamming (7,4) Code" ,Codeword 中 1 个数最少为 3,则 d=3;再结合前面说过的“最小距离作用”,可知 "Hamming (7,4) Code" 能够纠错 1 bit的错误。

Reed-Solomon code is (n,k) code with s-bit symbols. This means that the encoder takes k data symbols of s bits each and adds parity symbols to make an n-symbol codeword. There are n−k parity symbols of s bits each. A Reed-Solomon decoder can correct up to t symbols that contain errors in a codeword, where 2t=n−k
汉明码
汉明码编码
汉明码是将输入的信息位 [a b c d] 编码为 [a b c d x y z],结合生成矩阵表示如下:
其中,前四列是 Identity Matrix,作用是复制 abcd;后三列负责生成校验位,倒数第三列对应 x=a⊕b⊕d,倒数第二列对应 y=a⊕c⊕d,最后一列对应 z=b⊕c⊕d,
汉明码生成矩阵示例,Message 是 1101:
汉明码解码
the Parity-Check Matrix H is a tool that we use to correct errors:
如果 c 是 valid code word, 那么两者相乘得 0 : HcT=0⃗。
反之,如果 c is invalid, the output is nonzero。
Hamming (7,4) code 的奇偶检验矩阵推导如下 :
一、原始等式
二、右边为0
将等号右边移到等号左边得
三、异或表示
由于是二进制,减法运算等同于异或运算(原因可见下面模运算部分),
四、矩阵表示
属于 Linear Equations,用矩阵表示
例子:codeword c=[1 1 0 1 1 0 0],Hc⃗T=0⃗:
c⃗T 的 1st, 2nd, 4th, 5th 为 1,表示将 H 中的 1st, 2nd, 4th, 5th 列进行相加,这4列每一行加完后都是偶数,since we're using these ⊕ operation for addition, the result is a column of all zeros。结果为 0 说明 1101100 是 valid codeword。
if we take this valid codeword and add an error vector, we distribute the H matrix,
when we distribute the H matrix we find that the part with the valid codeword goes to 0 by definition(Hc⃗T=0) , so we're left with only the error term. 这个向量称为 syndrome vector(症候向量),能够反映出错的信息。
取上述例子的 code word vector c⃗=[1 1 0 1 1 0 0],加上一个表示 2nd 比特翻转的 error vector e⃗=[0 1 0 0 0 0 0],接受到的 vector 为 r⃗=[1 0 0 1 1 0 0], H 与 r⃗ 相乘的结果等于H 与 e⃗ 相乘,可得 [1 0 1],这个向量就是syndrome vector。该向量与 H 的 2nd 列一致,说明是 2nd bit 发生翻转。 由此可以还原出原始的信息。
Reed-Solomon
历史发展

结论:
理论早于应用 (LDPC也是一样)
Reed-Solomon有两个分支,一种是原始观点,一种BCH观点。BCH观点的为主流。
插值定理
拉格朗日插值定理指出:给定 n+1 个互不相同的点 (x0,y0),(x1,y1),\dots,(xn,yn),存在唯一的次数不超过 n 的多项式 P(x) 通过所有这些点。 (可用反证法证明其唯一性)
虽然拉格朗日插值通常使用拉格朗日基函数来构造,但我们可以用高斯消元法来求解系数,这样更直观地理解"确定唯一多项式"的过程。
对于 n+1 个点,我们要找多项式:P(x)=anxn+an−1xn−1+\dots+a1x+a0
使得 P(xi)=yi 对所有 i=0,1,\dots,n 成立。
这给出线性方程组:
矩阵形式为 Va=y,其中 V 是范德蒙德矩阵(Vandermonde)。
随机的2个点可确定唯一一个 f(x)=ax+b
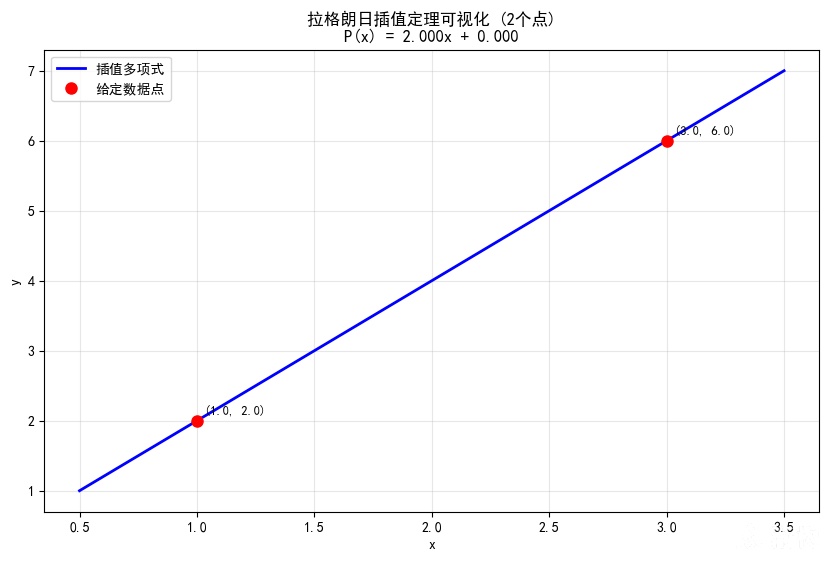
随机的3个点可确定唯一一个 f(x)=ax2+bx+c

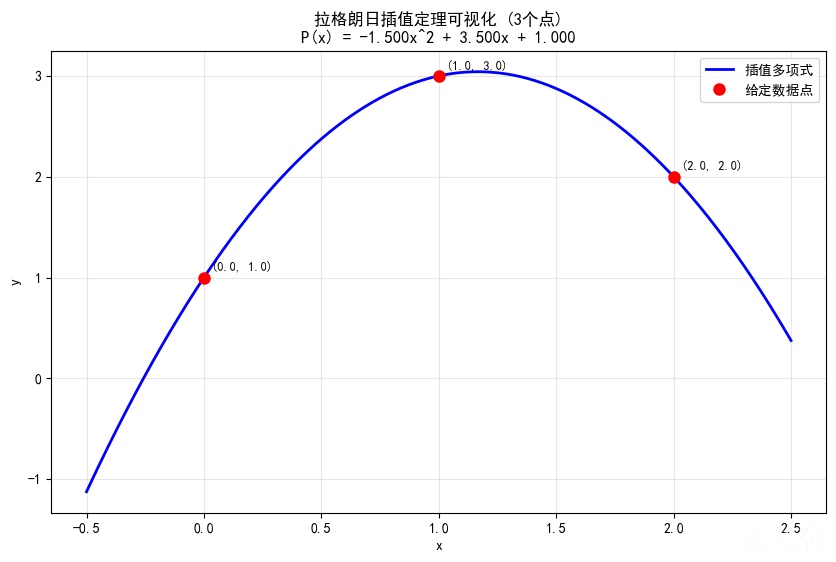
随机的4个点可确定唯一一个 f(x)=ax3+bx2+cx+d
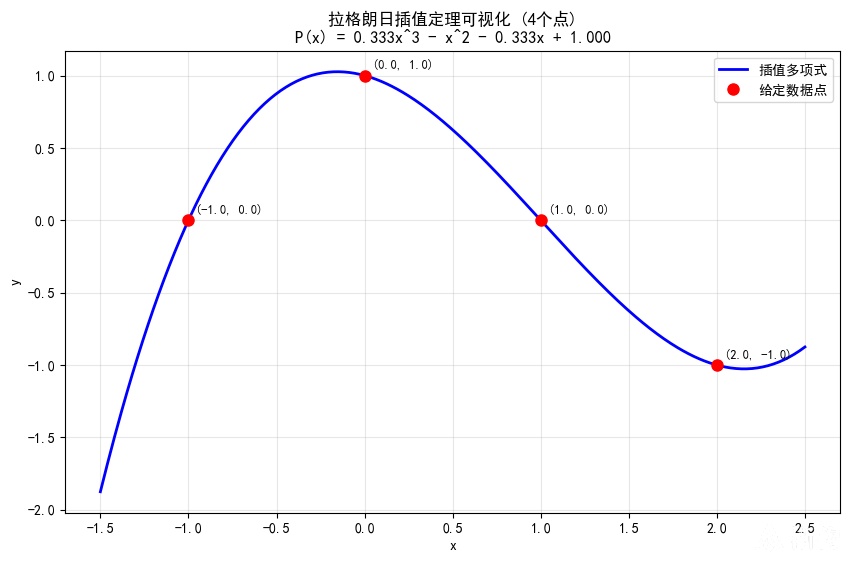
假设有3个点: (0, 1), (1, 3), (2, 2),求唯一的最高次项为2的多项式: f(x)=a0∗x2+a1∗x+a2。代入3个点的值,得到:
f(0)=a0∗02+a1∗0+a2=1
f(x)=a0∗12+a1∗1+a2=3
f(x)=a0∗22+a1∗2+a2=2
用矩阵表示为:
用高斯消元法即可求出a0,a1,a2。
原始消息: [10, 25, 30, 15],构成4个点 (0, 10), (1, 25), (2, 30), (3, 15),然后构建出一个唯一的多项式,再取 x=4, x=5, x=6 时y的三个取值。
生成7个份额: [10.0, 25.0, 30.0, 15.0, -30.0, -115.0, -250.0]
假设丢失了3个份额,索引为: [0, 1, 5]
剩余份额: [(2, 30.0), (3, 15.0), (4, -30.0), (6, -250.0)],根据拉格朗日插值定理,我们可以重构出相同的唯一的多项式。根据这个多项式,也就能还原出原始消息: [10.0, 25.0, 30.0, 15.0]
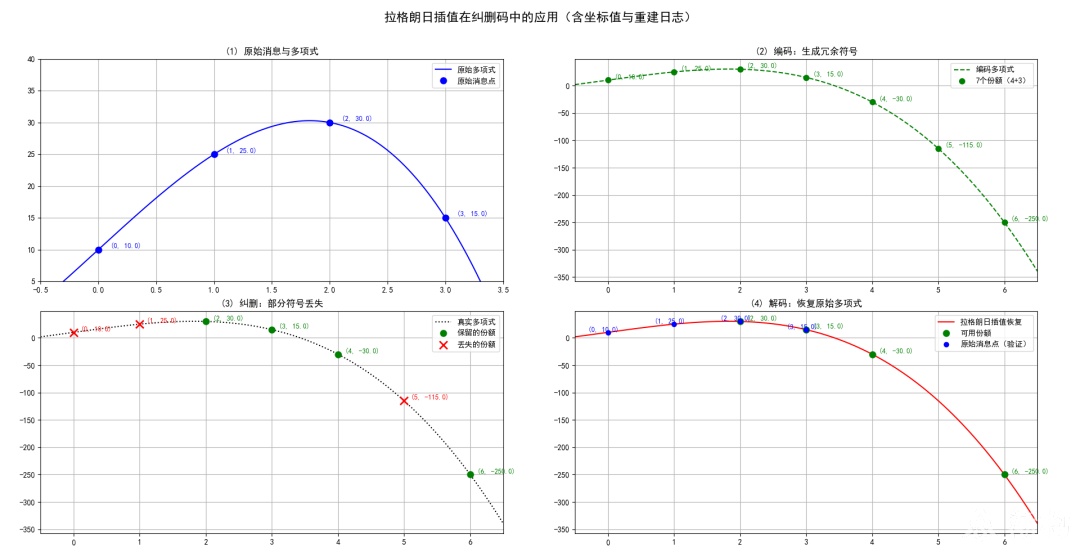
但是这种计算方式会使得数值过大,无法应用。我们希望:
编码不用大整数 (n−1)k−1 , 解码不用浮点数。
codeword symbol 的取值范围最好和 message symbol 一样,都是字节 [0, 255]。这就要用到 Finite Field,也叫 Galois Field 迦罗华域。
暴力遍历求解: https://tomverbeure.github.io/2022/08/07/Reed-Solomon.html
Encoder
Create polynomial p(x)=2+3x−5x2+x3. It uses the message word symbols as coefficients.
Evaluate the polynomial p(x) at the 6 locations of x: (−1,7),(0,2),(1,1),(2,−4),(3,−7),(4,−2).
The code word is: (7,2,1,−4,−7,−2)
Decoder
The decoder received the following code word: (7,2,6,−4,−7,−2).
Associate each symbol with its corresponding x value: (−1,7),(0,2),(1,6),(2,−4),(3,−7),(4,−2).
From these 6 coordinates, draw all combinations of 4 elements:
(−1,7),(0,2),(1,6),(2,−4)
(−1,7),(0,2),(1,6),(3,−7)
(−1,7),(0,2),(1,6),(4,−2)
(−1,7),(0,2),(2,−4),(3,−7)
(−1,7),(0,2),(2,−4),(4,−2)
(−1,7),(0,2),(3,−7),(4,−2)
(−1,7),(1,6),(2,−4),(3,−7)
(−1,7),(1,6),(2,−4),(4,−2)
(−1,7),(1,6),(3,−7),(4,−2)
(−1,7),(2,−4),(3,−7),(4,−2)
(0,2),(1,6),(2,−4),(3,−7)
(0,2),(1,6),(2,−4),(4,−2)
(0,2),(1,6),(3,−7),(4,−2)
(0,2),(2,−4),(3,−7),(4,−2)
(1,6),(2,−4),(3,−7),(4,−2)
There are 15 combinations.
For each of these 15 combinations, determine the 4 polynomial coefficients:
(−1,7),(0,2),(1,6),(2,−4)→(2,8,−5/2,−3/2)
(−1,7),(0,2),(1,6),(3,−7)→(2,27/4,−5/2,−1/4)
(−1,7),(0,2),(1,6),(4,−2)→(2,19/3,−5/2,1/6)
(−1,7),(0,2),(2,−4),(3,−7)→(2,3,−5,1)
(−1,7),(0,2),(2,−4),(4,−2)→(2,3,−5,1)
(−1,7),(0,2),(3,−7),(4,−2)→(2,3,−5,1)
(−1,7),(1,6),(2,−4),(3,−7)→(19/2,17/4,−10,9/4)
(−1,7),(1,6),(2,−4),(4,−2)→(26/3,14/3,−55/6,11/6)
(−1,7),(1,6),(3,−7),(4,−2)→(7,61/12,−15/2,17/12)
(−1,7),(2,−4),(3,−7),(4,−2)→(2,3,−5,1)
(0,2),(1,6),(2,−4),(3,−7)→(2,18,−35/2,7/2)
(0,2),(1,6),(2,−4),(4,−2)→(2,49/3,−15,8/3)
(0,2),(1,6),(3,−7),(4,−2)→(2,13,−65/6,11/6)
(0,2),(2,−4),(3,−7),(4,−2)→(2,3,−5,1)
(1,6),(2,−4),(3,−7),(4,−2)→(2,3,−5,1)The coefficients (2,3,−5,1) come up 6 times. All other solutions are different from each other, so (2,3,−5,1) is the winner. This is also the correct solution.
迦罗华域
模运算
在讲伽罗华域前,先讲下模运算:模运算,通常表示为"mod",是数学中的一种运算,它返回两个数相除后的余数。
模12运算,取值为 0~11。加法相当于顺时针,减法相当于逆时针。比如,假设现在是1点,
过了15小时,相当于顺时针走15步,就到了第2圈的4点,数学表达式为 1+15=4(mod 12)。
过去2小时,相当于逆时针走2步,就到了11,数学表达式为 1-2=11(mod 12)。
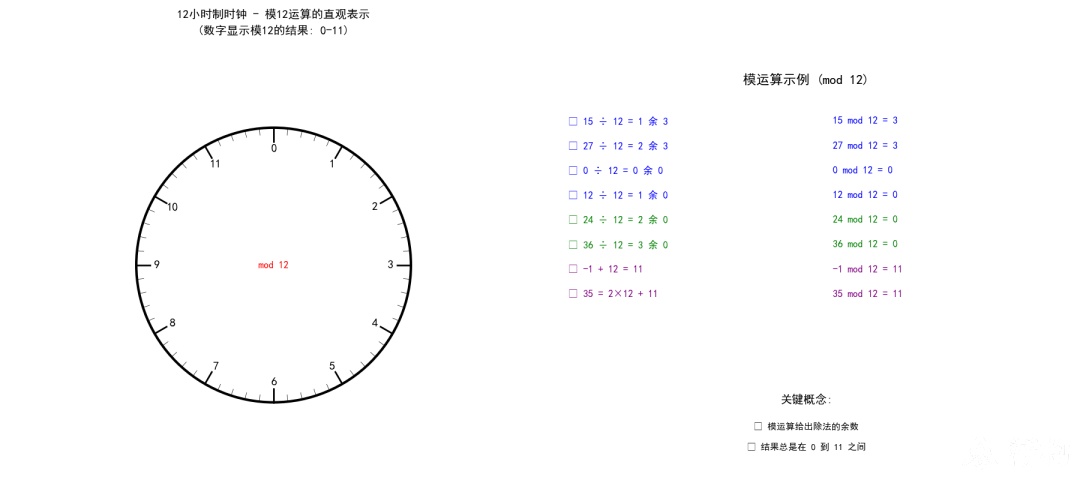
套用该“时钟模型”可知,当模为2时,则顺时针走一步与逆时针走一步所指向的数字是一样的(都是刚好走了半圈)。这就是说,模2运算的加法等同于减法:
0 + 0 = 0, 0 - 0 = 0
0 + 1 = 1, 0 - 1 = 1
1 + 0 = 1, 1 - 0 = 1
1 + 1 = 0, 1 - 1 = 0
这又刚好等价于异或运算。因此,在模2运算中,加法 = 减法 = 异或(异或在电路上易实现)。
伽罗华域
伽罗华域是由法国数学家埃瓦里斯特·伽罗华(Évariste Galois)提出的一种有限域(Finite Field),即包含有限个元素的代数结构,在该结构中可以进行加、减、乘、除(除0外)运算,并且结果仍然落在该集合内: 0,α0,α1,α2,...,αN−1。其中 α 为素数,通常取2,N=2m−1,这个域记作GF(2m)。
常见的 Reed-Solomon 编码使用的是 GF(2m) 型的域,例如:
GF(256)=GF(2^8) (集合里的元素为 0~255,计算结果仍落在该集合内)
GF(16)=GF(2^4) (集合里的元素为 0~15,计算结果仍落在该集合内)
为什么 Reed-Solomon 使用 GF(2m)?因为Reed-Solomon 编码处理的是符号(symbol),而不是单个比特。每个符号通常是一个字节(8 比特),因此自然对应到 GF(2⁸),它恰好有 256 个元素(0 到 255),可以用一个字节表示。
在 GF(2m) 中:元素可以表示为长度为 m 的二进制向量,或多项式$\alpha_{m-1}x{m-1}+...+\alpha_{1}x + \alpha_{0}$;
以 GF(16) 为例,此时 m = 4,多项式为: α3x3+α2x2+α1x1+α0x0。 α3α2α1α0 的取值范围为二进制的 0000 到 1111 共16个值。
多项式的加、减、乘、除、取余等运算: https://downloads.bbc.co.uk/rd/pubs/whp/whp-pdf-files/WHP031.pdf 第2章 Galois fields
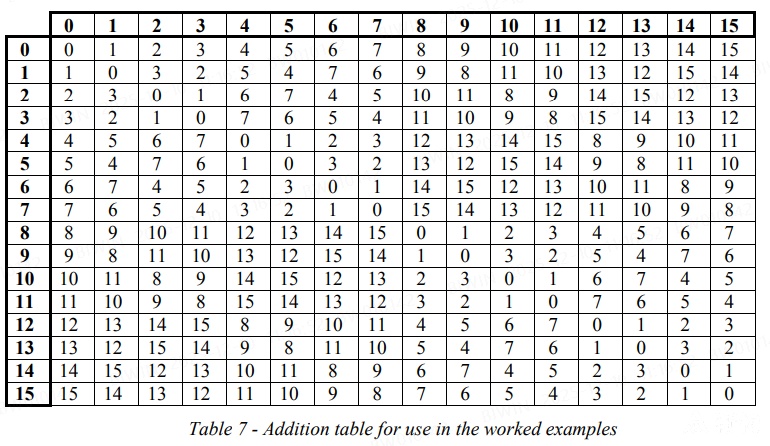
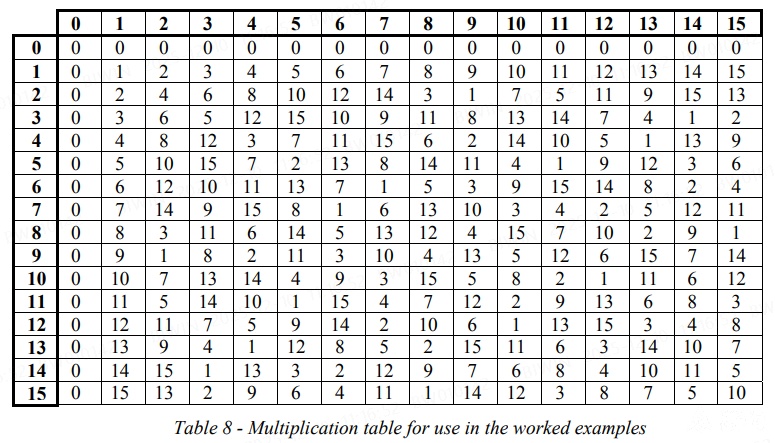
Tables 7 and 8 below show the results for addition of two field elements (Table 7) and multiplication of two field elements (Table 8) in the sixteen element Galois field with the field generator polynomial p(x)=x4+x+1。
注意到,加法、乘法的结果都在 0~15 之间。
RS编码
https://www.nayuki.io/page/reed-solomon-error-correcting-code-decoder 其中的 Systematic encoder
https://downloads.bbc.co.uk/rd/pubs/whp/whp-pdf-files/WHP031.pdf 其中的 1.1.2 Forming the code word

message: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11
message polynomial: x10+2x9+3x8+4x7+5x6+6x5+7x4+8x3+9x2+10x+11
乘以 x4,得 x14+2x13+3x12+4x11+5x10+6x9+7x8+8x7+9x6+10x5+11x4
除以 g(x)=(x+α0)(x+α1)(x+α2)(x+α3)=(x+1)(x+2)(x+4)(x+8)=x4+15x3+3x2+x+12

(图中的加法与乘法见伽罗华域内容里的两张表)
得到 remainder: r(x)=3x3+3x2+12x+12
由此构成要发送的信息T(x)=x14+2x13+3x12+4x11+5x10+6x9+7x8+8x7+9x6+10x5+11x4+3x3+3x2+12x+12,即1,2,3,4,5,6,7,8,9,10,11,3,3,12,12
RS出错
R(x) = T(x) + E(x)
注: R-receive, E-error
E(x)=En−1xn−1+...+E1x+E0
2 个 symbol 出错, E(x)=E9x9+E2x2,E9=13,E2=2
即,接受到的信息为: 1, 2, 3, 4, 5, 11, 7, 8, 9, 10, 11, 3, 1, 12, 12
RS解码
BCH视角下 reed-solomon 码的解码流程:
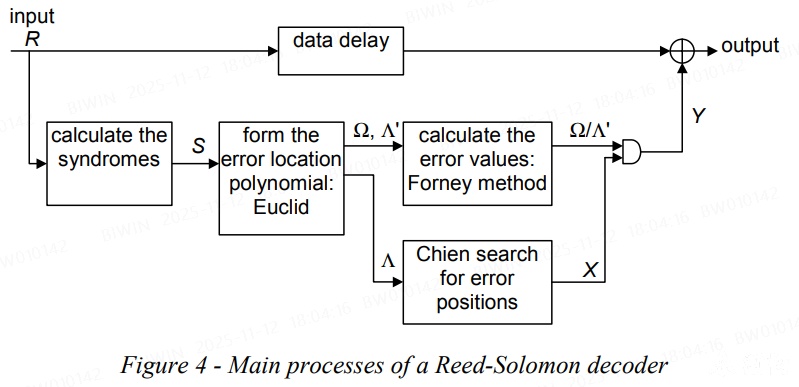
(15,11)code示例(对其中步骤的输入输出有个大概的判断即可,暂时不纠结具体的计算方式):
message: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11
encoding message: 1,2,3,4,5,6,7,8,9,10,11,3,3,12,12 (T(x)=x14+2x13+3x12+4x11+5x10+6x9+7x8+8x7+9x6+10x5+11x4+3x3+3x2+12x+12)
Error: 假设有2个symbol出错,E9=13,E2=2
receive: R = 1, 2, 3, 4, 5, 11, 7, 8, 9, 10, 11, 3, 1, 12, 12
calculate the syndromes: S0=15,S1=3,S2=4,S3=12
form the error location polynomial(Euclid): S(x)=12x3+4x2+3x+15 -> Λ(x)=14x2+14x+1,Ω(x)=6x+15.
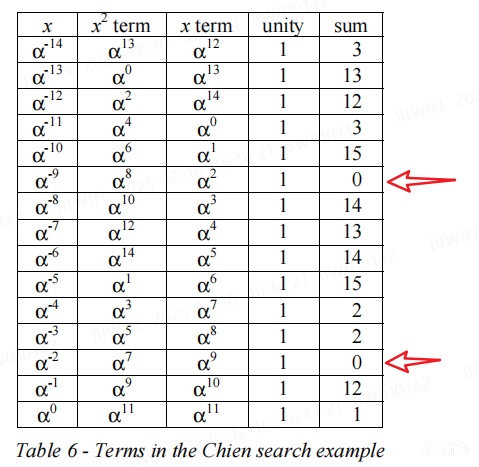
Chien search for error positions: 计算出值为0的位置就是出错的位置,见下表
caluculate the error values(Forney method): 位置9的值为13, 位置2的值为 2 -> 与上述 Error 一致
将计算出的结果与 R 相加就还原得到原始的 message