上料用法

一个完整的知识必然是立体的上下结构，若仅仅只是上层，则知识会悬空，仅仅只是下层，则知识会坍缩为经验，所以上料用法，一定绕不开建立完整的上下结构。

此外，既然是上料，那么一定是从“上”到“上”的方式。从什么“上”呢？只能从已有的完整的上下结构中的上层出发去达到待学的上下结构的上层。

那么待学概念的下层咋办？因为是从已有的完整的上下结构而来，所以待学的下层也会”继承“。

既然是从已有的来，那么怎么来？

1.直接对已有的上下结构中的上层进行”限定“，”组合“，形成新的上下结构。

2.间接对待学的新概念的上层进行”限定“等。

由于都是从上层出发，达到未见上层。所以小节名字也叫做上料用法。

开篇讲到语言，为什么说上料用法是借助了语言的跨时空能力呢？

想象一下，假设你我没有语言，不能说话，不能写字，不能想象，那么概念只能在具体的情景中做出触发。

例如，只有实际碰到老虎，才能做出反应。

但语言的出现，使得老虎可以化作符号，用于事先或事后谋划，谋划就是跨时空所呈现的。

并且这种符号化的想象能力，使得虚幻成为可能。龙，吸血鬼，变形金刚等都是虚幻的。

既然是从未见过的，虚幻的，现实中连对象都不存在的，何谈上下结构呢？

在《人是如何学习的》这本书中有一个例子，青蛙与鱼，鱼一生都生活在水里，青蛙是鱼的好朋友，青蛙经常给鱼讲陆地上的生活，陆地上有人，人是两足直立，而且身上的衣服颜色非常多，鱼只能理解人是由两个鳍，直着游的，鱼鳞颜色非常多这么一个生物。

人超出了鱼的经验，而理解这样一个超经验的概念，鱼也只能通过对已有概念的组合进行理解。

上文讲了通过“改造”已有的上下结构，得到新的上下结构。而这种特点是我们==直接==对上层进行“改造”。

此外，还有一种现象，没有直接对上层进行”改造“，通过不断限定，不断约束，最终汇聚“一点”从而明确待学概念的上层，即词络约束。

二者都符合从“上”到“上”，不过其方式不同。用韦恩图表示如下：



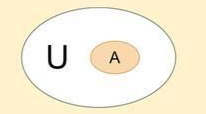
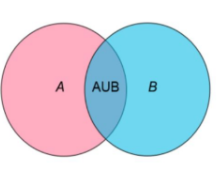
无论是重组还是约束，都可以用这两种方式理解。

例如：
偶数，可以用第一个韦恩图理解，所有的数对应的是 ==U== （自然数，正数，分数，小数，正数，负数，有理数，无理数，实数，虚数等），不断的限定约束进而得到偶数 ==A==。

也可以用第二个韦恩图理解，即所有的整数==A==（负整数，正整数等）与可以被2整除的数==B==，偶数就是A与B相互重合的部分。

同理，小节所有的例子都可以用这两种方式理解。

自上前提

前文说到，上料用法是从已知入手，达到未知，既然是已知，那么默认基本概念都是掌握的。

万一不懂咋办？说明上下结构中上层是缺失了，或者整个上下结构都缺失了，面对这种情况，自下兜底！

至于后文的语法规则，表达转换，行为目标与上文讨论的核心不同，这里就不说明了。