数学的魔法性

公理不等于事实，由公理所支撑的这部分数学，是一个魔法世界。

虽然抽象且脱离事实，但这种抽象的关系，配合将事物抽象的能力。例如将事物量化，量化后进行推导运算。


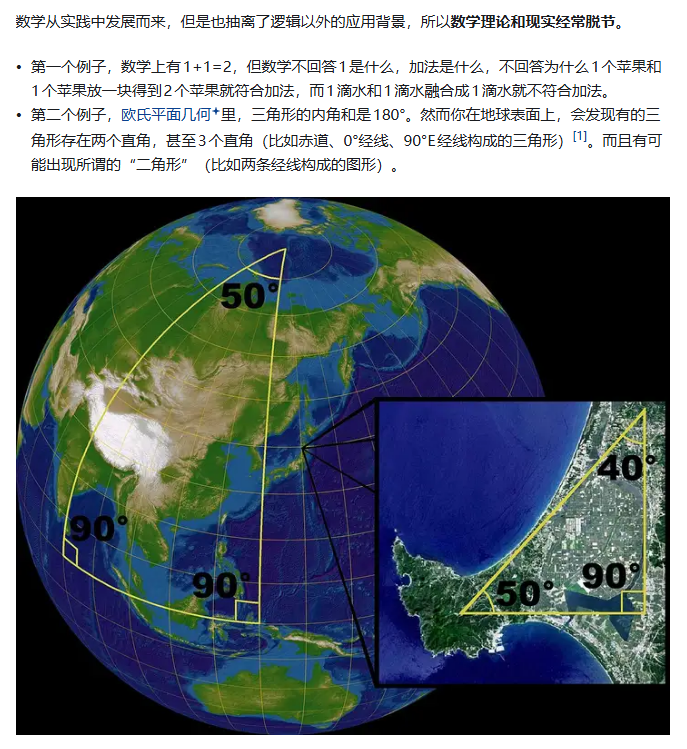
已知，超验，理解

数字，人为创造的。在如何理解数字时，可以通过==感性的，隐喻的==方式理解。例如大小，长短，运算，角度等概念，可以形象的用实际物体的高矮，大小理解，运算以游戏规则理解，角度以岔开程度等理解。

==一切思维皆隐喻，这句话的另外一层含义就是，我们不可能用连我们自身都没见过，感受过的东西来描述和呈现==。

从上面的标黄段落可以推出一个议题，那些我们从未见过，从未感受过的东西是否可以被认知，即超验概念是否可以被理解。

按照康德的答案，无法理解


按照超验的思路继续延申，如何理解未知概念呢？既然无法从未知到未知，那么只能从已知到未知。

这里的已知怎么来？

如果是具体对象，那就展现具体对象，拿出这个东西，或者用文图等方式呈现。

如果是抽象对象，那就需要用已知的东西进行”拼凑“，例如原子，圆圈都是已知的，通过赋予圆圈一些属性（例如电子），增加一些规则（例如互斥），进而”拼凑“出未知概念。


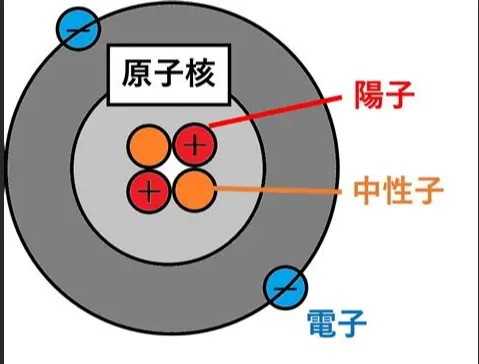
已知到未知的视角也可以用于理解课程所讲的==词络约束，旧义重组==。