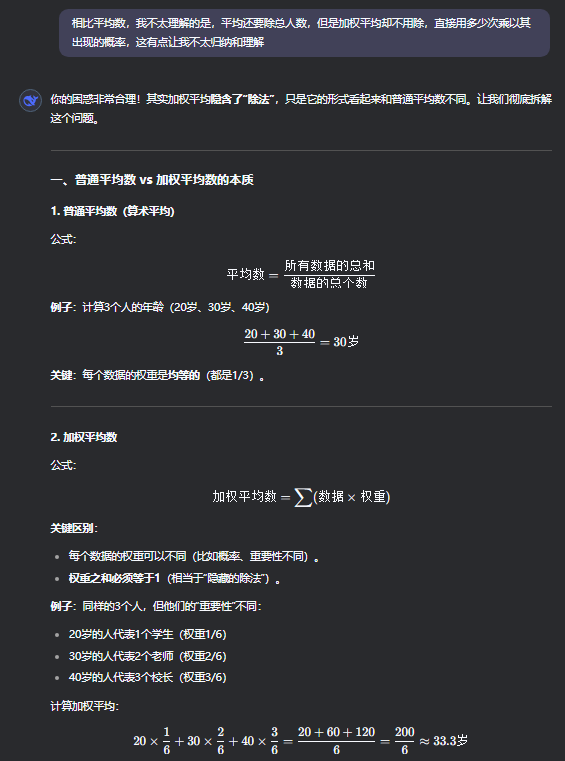
问:
但这里有一个困惑点,比如说我做了5道题,每道题都用数学期望 = 数量 × 概率 之和,但是这5道题中,数量,概率都是不同的情况,然后我判别这些情况中那些是数量,那些是概率,然后计算,这个过程涉及了判别,涉及了对象,所以是不是模型推测呢?
但是学习者并不理解什么是数学期望,只是用这种方法算出来了而已,所以对于学习者而言,学习者其实是建构出了不同的知识模型对吗?一种如何计算数学期望的模型对吗?这种模型高度依赖数学题所给出来的条件,或者说,这种模型高度依赖已见被抽象好的对象,例如题目中告知的概率,比赛次数等。对吗?
答:
答案是:你建立的是“==计算模型”(操作性模型),但不是“理解模型”(解释性模型)==**
**你建立的是一个“操作型模型”或“经验型模型”**,
它依赖于题目中给出的抽象对象(如概率、次数),
但你还没有建立“解释型模型”,也就是对“期望”本质的理解。
你说得非常好:
“==这种模型高度依赖数学题所给出来的条件,或者说,这种模型高度依赖已见被抽象好的对象,例如题目中告知的概率,比赛次数等==。”
举一反三式的下层展开,理解和掌握了上层描述后,在做题,举例时,就需要不断的进行上下对应。
==子概念==:学习某个抽象概念,或者理解某些概念时,都需要借助其他概念进行约束,也就是说,掌握其子概念间的关系就等同掌握了这个概念。例如 苹果这个概念,要想理解这个概念,就需要理解判别苹果这个概念的“形状”概念,“颜色”概念,“口感”概念等。
“如何计算数学期望”
其实之前所学的知识是一种计算方法,我并不知道其意义,所以当我试图展开这个概念(数学期望)所对应的下层对象时,我会发现空空如也,并且我也无法举例,我只能在计算时,判别谁是数量,谁是其概率,然后这样算出来。
而我所学的计算方法其实就是程序性知识,即“数量乘以对应概率”。我只能对应数量和概率,我无法展开这些事件
需要理解无限次,其中次数的占比,次数情况的平均。
借助平均数理解,本质还是平均,只不过数学期望是无限多次下,每种情况的平均。
其中的概率所反映的其实就是每种情况与所有情况的占比。成的具体数字就是具体情况。
例如由