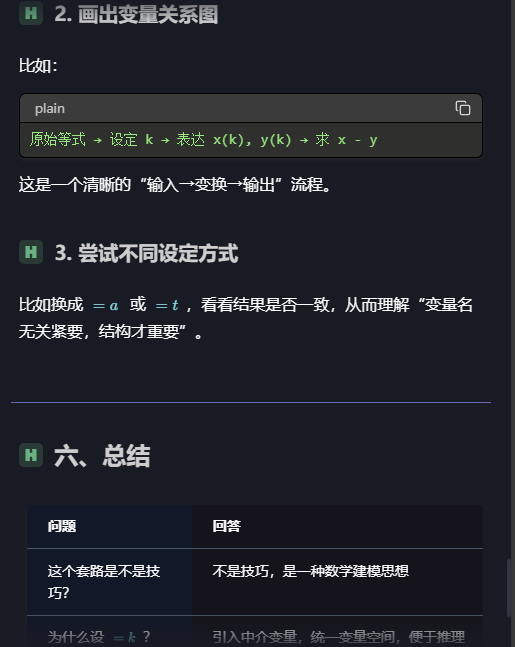
选择不同的概念或者规律去归纳源于之前我的一段体悟,即我可以外显化的用符号指代概念。
我可以用符号操控这些概念在我的意识中,所以当我归纳错的时候我可以溯源,是我选取的某些概念不对。
我发现一个现象,我觉得和课程中这句话有很大的关系,“「自下学习」的过程中,也可以运用「其它知识的演绎和类推」,并无思维方式的限制,只不过这些方式最终会服务于「目标知识的归纳」。” 现象如下,我在学习高中数学知识时,我发现我在总结题目会归纳到不同的概念中去,例如
在和AI问答时候,我困惑为什么看到连等的式子,直接令这个连等的式子=k,就行了,这似乎是一种技巧,其背后有什么具体的思想嘛?这些思想我是否学过?
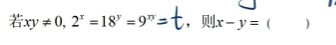
下面的两个问答,我更倾向于豆包的回答,即这种技巧本质上是指数对数的转化技巧,或者说是是对数计算公式的一种拓展,要说其思想,本质上是化归思想。
==因为对数的运算,最初就是对于指数的一种简化==。
==同时这也说明了,我在归纳的时候所采用的是什么“概念”,如果是“新参数”,“新方程”那么可能会引导我向相关方向思考;若采用的是“指数与对数的转换”那么就符号这一章节所讲的。==
==而且,从以上的启发,加上下面的学会的表征,我可以把我的归纳过程显化出来,即用图来,意识到我最初试图归纳的概念是什么”盒子“(是新参数,新方程;还是指数与对数的转换),选择不同的概念进行处理,会导致我产生概念遮蔽,即思想困在这么一条道上了==。
我:
我的困惑源于,高中时候会遇到这样的题,
豆包: